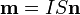Campo producido por una espira poligonal
De Laplace
(→Campo en P) |
(→Momento magnético) |
||
| Línea 41: | Línea 41: | ||
===Momento magnético=== | ===Momento magnético=== | ||
| + | El [[Desarrollo_multipolar_magnético#Espira_plana|momento magnético de una espira plana]] es | ||
| + | |||
| + | <center><math>\mathbf{m}=IS\mathbf{n}</math></center> | ||
| + | |||
==Espira alabeada== | ==Espira alabeada== | ||
===Campo en P=== | ===Campo en P=== | ||
===Momento magnético=== | ===Momento magnético=== | ||
[[Categoría:Problemas de campo magnético de corrientes estacionarias]] | [[Categoría:Problemas de campo magnético de corrientes estacionarias]] | ||
Revisión de 15:38 20 abr 2009
Contenido |
1 Enunciado
Por las espira de formas irregulares de las figuras circula una corriente I. Halle el valor del campo en el punto P en cada caso.
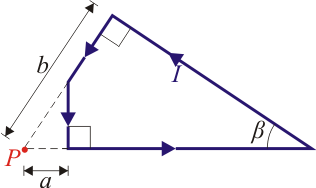
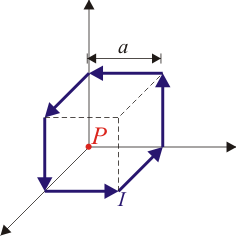
Para cada una de las espiras, hállese su momento magnético y la expresión del campo magnético y del potencial vector en puntos alejados de la espira.
2 Cuadrilátero
2.1 Campo en P
El campo es la suma de las contribuciones de cada uno de los lados del cuadrilátero. El campo de un segmento puede calcularse por integración directa, resultando la expresión
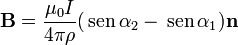
donde α1 y α2 son los ángulos con que se ven los extremos del segmento desde P, ρ es la distancia de P a la recta soporte del segmento y 
la normal al plano definido por el segmento y P, orientado según la regla de la mano derecha.
Quedan las contribuciones de los otros dos lados.
Para el lado situado a una distancia a tenemos que
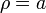
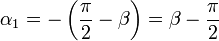
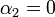
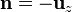
es el vector perpendicular al plano de la espira, hacia adentro de la pantalla. La contribución de esta lado es
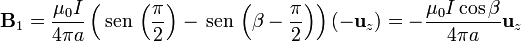
Para el lado situado a una distancia b tenemos que
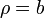
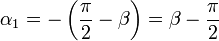
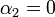
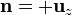
La contribución de esta lado es
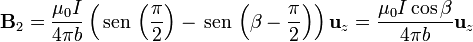
y el campo en P
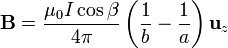
Puesto que a < b, este campo va hacia adentro de la pantalla.
2.2 Momento magnético
El momento magnético de una espira plana es
