Resistividad
De Laplace
(→Valores típicos) |
(→Unidades) |
||
| Línea 9: | Línea 9: | ||
==Unidades== | ==Unidades== | ||
| - | De la definición, se tiene que la unidad en el SI de la resistividad es 1 Ω& | + | De la definición, se tiene que la unidad en el SI de la resistividad es 1 Ω·m. Para los conductores metálicos, que poseen resistividades muy bajas, se usan submúltiplos, como 1 nΩ·m, o 1 μΩ·cm. |
==Ley de Joule== | ==Ley de Joule== | ||
última version al 17:50 9 abr 2009
Contenido |
1 Definición
Se define la resistividad, r (o ρ), como la inversa de la conductividad,
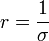
esto es, en los materiales óhmicos, es la constante de proporcionalidad entre el campo eléctrico y la densidad de corriente
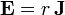
2 Unidades
De la definición, se tiene que la unidad en el SI de la resistividad es 1 Ω·m. Para los conductores metálicos, que poseen resistividades muy bajas, se usan submúltiplos, como 1 nΩ·m, o 1 μΩ·cm.
3 Ley de Joule
Empleando la resistividad, la potencia disipada por efecto Joule por unidad de volumen queda en términos de la densidad de corriente
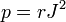
y la potencia total disipada
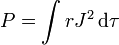
4 Conductor filiforme
La resistencia de un cable es proporcional a su resistividad
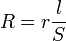
5 Valores típicos
Como la conductividad, la resistividad posee un amplísimo rango de variación. Para materiales metálicos, de baja resistividad, algunos valores son
| Material | r (1 nΩ·m) |
|---|---|
| Plata | 15.87 |
| Cobre | 16.78 |
| Oro | 22.14 |
| Hierro | 96.1 |
Un tipo especial de materiales lo constituyen los superconductores para los cuales la resistividad es idénticamente nula, por debajo de una cierta temperatura crítica





