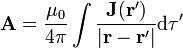Ley de Gauss para el campo magnético
De Laplace
(Diferencias entre revisiones)
(→Forma diferencial) |
(→Forma diferencial) |
||
| Línea 4: | Línea 4: | ||
y, operando se llega a que puede escribirse como | y, operando se llega a que puede escribirse como | ||
| - | <center><math>\mathbf{B}=\nabla\times\mathbf{A}</math>{{qquad}}{{qquad}}<math>\mathbf{A}=\frac{\mu_0}{4\pi}\int\frac{\ | + | <center><math>\mathbf{B}=\nabla\times\mathbf{A}</math>{{qquad}}{{qquad}}<math>\mathbf{A}=\frac{\mu_0}{4\pi}\int\frac{\mathbf{J}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}\tau'</math></center> |
==Forma integral== | ==Forma integral== | ||
Revisión de 17:05 21 mar 2009
Contenido |
1 Forma diferencial
Para calcular la divergencia del campo magnético, se parte de la ley de Biot y Savart para una distribución de corriente de volumen
y, operando se llega a que puede escribirse como