Campo magnético de corrientes estacionarias
De Laplace
(→Fuerza sobre un circuito) |
(→Ley de Biot y Savart) |
||
| Línea 54: | Línea 54: | ||
| - | + | ||
| + | |||
==Fuentes del campo magnético. Ley de Ampère== | ==Fuentes del campo magnético. Ley de Ampère== | ||
==El potencial vector magnético== | ==El potencial vector magnético== | ||
Revisión de 18:26 20 mar 2009
Contenido |
1 Fuerza sobre una carga en movimiento
Se ve en electrostática que una carga puntual en reposo experimenta una fuerza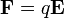 
. Si esta carga se encuentra en movimiento, debemos añadir una fuerza adicional, proporcional a la velocidad y ortogonal a ella, de acuerdo con la ley de Lorentz
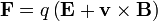
A esta fuerza adicional se la denomina fuerza magnética, y al campo vectorial 
, que da la magnitud de esta fuerza, se lo denomina campo magnético (también conocido como inducción magnética y como densidad de flujo magnético).
El campo magnético se mide en el SI en Teslas (T), siendo 1 T = 1 N/A·m. Un Tesla es una cantidad grande para los valores usuales, por lo que con frecuencia se usa como unidad el Gauss (1 Gauss = 0.0001 T).
La fuerza sobre una carga en movimiento puede extenderse a un conjunto de ellas, que formarán una densidad de corriente. Para el caso de una densidad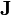 
, la fuerza magnética es
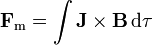
y análogamente se tiene la fuerza sobre una distribución de corriente superficial y sobre un conductor filiforme.
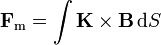
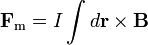
Si tenemos un conjunto de distribuciones, la resultante será la suma de la fuerza sobre cada una de ellas.
2 Campo magnético debido a una corriente
Los campos magnéticos pueden tener distintas causas. Entre ellas, se encuentran las propias corrientes eléctricas.
El campo magnético creado por una carga puntual en movimiento a velocidades bajas (comparadas con la de la luz) vale aproximadamente
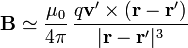
siendo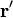 
la posición instantánea de la carga. μ0 es una constante denominada permeabilidad del vacío, cuyo valor en el SI es 
.
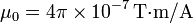El campo magnético creado por una distribuciónde corriente lineal puede calcularse integrando la expresión anterior. Para el caso de una corriente estacionario la aproximación se convierte en una igualdad y el campo magnético viene dado por la ley de Biot y Savart
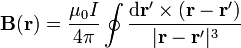
Un caso particular importante es el del hilo rectilíneo infinito que produce un campo
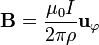
Este campo gira en torno al hilo, siendo circunferencias sus líneas de campo
También es importante el campo debido a una espira circular, que en los puntos de su eje vale
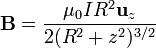
Este campo apunta en la dirección del eje de la espira, siendo máximo, con un valor μ0I / 2R en su centro.
De forma análoga al caso de la corriente lineal tenemos el campo creado por una distribución de corriente estacionaria volumétrica y por una superficial
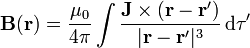
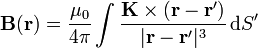
En estas expresiones las densidades de corriente son funciones de la posición,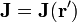 
,
.
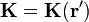