Campo magnético de corrientes estacionarias
De Laplace
(→Fuerza sobre una carga en movimiento) |
(→Fuerza sobre una carga en movimiento) |
||
| Línea 1: | Línea 1: | ||
==Fuerza sobre una carga en movimiento== | ==Fuerza sobre una carga en movimiento== | ||
| + | {{ac|Ley de Lorentz}} | ||
Se ve en electrostática que una carga puntual en reposo experimenta una fuerza <math>\mathbf{F}=q\mathbf{E}</math>. Si esta carga se encuentra en movimiento, debemos añadir una fuerza adicional, proporcional a la velocidad y ortogonal a ella, de acuerdo con la ''[[ley de Lorentz]]'' | Se ve en electrostática que una carga puntual en reposo experimenta una fuerza <math>\mathbf{F}=q\mathbf{E}</math>. Si esta carga se encuentra en movimiento, debemos añadir una fuerza adicional, proporcional a la velocidad y ortogonal a ella, de acuerdo con la ''[[ley de Lorentz]]'' | ||
Revisión de 11:40 18 mar 2009
Contenido |
1 Fuerza sobre una carga en movimiento
Se ve en electrostática que una carga puntual en reposo experimenta una fuerza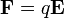 
. Si esta carga se encuentra en movimiento, debemos añadir una fuerza adicional, proporcional a la velocidad y ortogonal a ella, de acuerdo con la ley de Lorentz
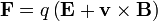
A esta fuerza adicional se la denomina fuerza magnética, y al campo vectorial 
, que da la magnitud de esta fuerza, se lo denomina campo magnético (también conocido como inducción magnética y como densidad de flujo magnético).
El campo magnético se mide en el SI en Teslas (T), siendo 1 T = 1 N/A·m. Un Tesla es una cantidad grande para los valores usuales, por lo que con frecuencia se usa como unidad el Gauss (1 Gauss = 0.0001 T).
La fuerza sobre una carga en movimiento puede extenderse a un conjunto de ellas, que formarán una densidad de corriente. Para el caso de una densidad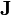 
, la fuerza magnética es
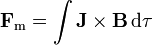
y análogamente se tiene la fuerza sobre una distribución de corriente superficial y sobre un conductor filiforme.
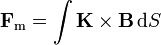
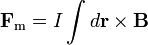
Si tenemos un conjunto de distribuciones, la resultante será la suma de la fuerza sobre cada una de ellas.
