Segunda Prueba de Control 2020/21 (G.I.C.)
De Laplace
(Diferencias entre revisiones)
(→Disco apoyado en dos esquinas) |
(→Partícula deslizando sobre disco con muelle) |
||
| Línea 15: | Línea 15: | ||
==[[ Partícula deslizando sobre disco con muelle (Ene. 2021 G.I.C.)| Partícula deslizando sobre disco con muelle ]]== | ==[[ Partícula deslizando sobre disco con muelle (Ene. 2021 G.I.C.)| Partícula deslizando sobre disco con muelle ]]== | ||
| + | [[File:F1GIC-particulaDiscoMuelle-enunciado.png|right]] | ||
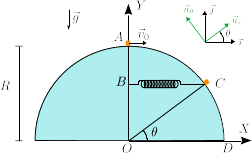
| + | Una partícula de masa <math>10m_0</math> desliza sin rozamiento sobre un semidisco de radio <math>R</math>. En el instante inicial la partícula se encuentra en el punto <math>A</math> y se le imparte una velocidad horizontal de rapidez <math>v_0=\lambda\sqrt{gR}</math>, siendo <math>\lambda</math> un número real positivo. La masa está conectada a un muelle de constante elástica <math>k=25m_0g/R</math> y longitud natural nula. El otro extremo del muelle está conectado al punto <math>B</math> que se mueve de modo que el muelle permanece siempre horizontal. | ||
| + | #Escribe los vectores de la base cartesiana en la base polar. | ||
| + | #Escribe la expresión de la fuerza ejercida por el muelle sobre la masa en la base polara. | ||
| + | #Escribe la expersión que da la velocidad de la partícula para el ángulo <math>\theta=\beta</math>, con <math>\mathrm{sen}\,\beta=3/5</math> y <math>\cos\beta=4/5</math>. | ||
| + | #¿Que condición debe cumplir <math>\lambda</math> para que la partícula se separe del disco en ese ángulo <math>\beta</math>? | ||
última version al 20:09 24 ene 2021
1 Disco apoyado en dos esquinas
El disco de la figura tiene masa 4m0 y radio R. El disco se apoya sobre dos esquinas. El contacto con la esquina A es liso mientra que con la esquina B es rugoso con coeficiente de rozamiento estático μ. El ángulo β verifica
Una fuerza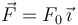 
actúa sobre el punto C.
- Dibuja el diagrama de cuerpo libre del disco.
- Encuentra el valor de las fuerzas que actúan sobre el disco en situación de equilibrio estático.
- ¿Para qué valor de F0 el disco empiece a rotar alrededor del eje que pasa por B?
- Si el valor de F0 es la solución del apartado anterior, ¿qué condición debe cumplir μ para que el disco no deslice en B?
2 Partícula deslizando sobre disco con muelle
Una partícula de masa 10m0 desliza sin rozamiento sobre un semidisco de radio R. En el instante inicial la partícula se encuentra en el punto A y se le imparte una velocidad horizontal de rapidez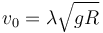 
, siendo λ un número real positivo. La masa está conectada a un muelle de constante elástica k = 25m0g / R y longitud natural nula. El otro extremo del muelle está conectado al punto B que se mueve de modo que el muelle permanece siempre horizontal.
- Escribe los vectores de la base cartesiana en la base polar.
- Escribe la expresión de la fuerza ejercida por el muelle sobre la masa en la base polara.
- Escribe la expersión que da la velocidad de la partícula para el ángulo θ = β, con
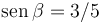y cosβ = 4 / 5.
- ¿Que condición debe cumplir λ para que la partícula se separe del disco en ese ángulo β?
