De Laplace

1 Enunciado

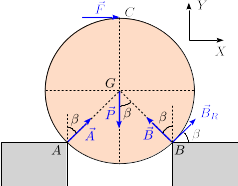
El disco de la figura tiene masa $4 m 0$ y radio $R$ . El disco se apoya sobre dos esquinas. El contacto con la esquina $A$ es liso mientra que con la esquina $B$ es rugoso con coeficiente de rozamiento estático $μ$ . El ángulo $β$ verifica

$\cos\beta = 3/5, \qquad \mathrm{sen}\,\beta=4/5.$

Una fuerza 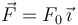$\vec{F}=F_0\,\vec{\imath}$ actúa sobre el punto $C$ .

Dibuja el diagrama de cuerpo libre del disco.
Encuentra el valor de las fuerzas que actúan sobre el disco en situación de equilibrio estático.
¿Para qué valor de $F 0$ el disco empiece a rotar alrededor del eje que pasa por $B$ ?
Si el valor de $F 0$ es la solución del apartado anterior, ¿qué condición debe cumplir $μ$ para que el disco no deslice en $B$ ?

2 Solución

La figura de la derecha muestra las fuerzas que actúan sobre el disco. En cada esquina hay dos fuerzas vinculares radiales que se encargan de que el disco no penetre en la esquina. En el punto $B$ hay además una fuerza de rozamiento que intenta impedir que el disco resbale sobre la esquina derecha.

Las expresiones de las fuerzas son, observando donde aparece el ángulo $β$ en la figura,

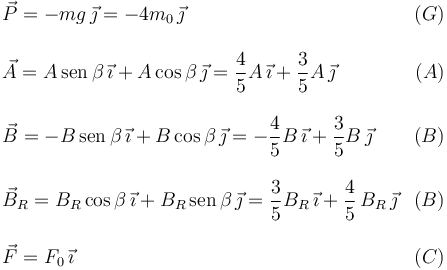
$\begin{array}{lr} \vec{P} = -mg \,\vec{\jmath} = -4m_0\,\vec{\jmath} & (G)\\ &\\ \vec{A} = A\,\mathrm{sen}\,\beta\,\vec{\imath} + A\cos\beta\,\vec{\jmath} = \dfrac{4}{5}A\,\vec{\imath} + \dfrac{3}{5}A\,\vec{\jmath}& (A)\\ &\\ \vec{B} = -B\,\mathrm{sen}\,\beta\,\vec{\imath} + B\cos\beta\,\vec{\jmath} = -\dfrac{4}{5}B\,\vec{\imath} + \dfrac{3}{5}B\,\vec{\jmath}& (B)\\ &\\ \vec{B}_R = B_R\cos\beta\,\vec{\imath} + B_R\,\mathrm{sen}\,\beta\,\vec{\jmath} =\dfrac{3}{5}B_R\,\vec{\imath} + \dfrac{4}{5}\,B_R\,\vec{\jmath} & (B)\\ &\\ \vec{F} = F_0\,\vec{\imath} & (C) \end{array}$

Tenemos tres incógnitas: ${A, B, B R}$ . Aplicamos las condiciones de equilibrio.

Sumatorio de fuerzas nulo

Obtenemos dos ecuaciones

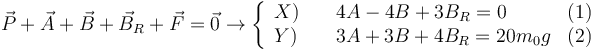
$\vec{P} + \vec{A} + \vec{B} + \vec{B}_R + \vec{F} = \vec{0} \to \left\{ \begin{array}{llr} X)\quad& 4A -4B + 3B_R = 0 & (1)\\ Y)\quad& 3A + 3B + 4B_R = 20m_0g & (2) \end{array} \right.$

Momento neto de fuerzas nulo

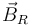Calculamos el momento respecto del punto $G$ . Sólo las fuerzas $\vec{F}$ y $\vec{B}_R$ crean momento respecto de este punto.

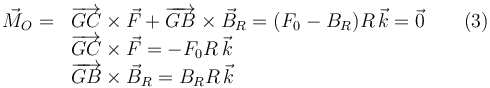
$\begin{array}{ll} \vec{M}_O = & \overrightarrow{GC}\times\vec{F} + \overrightarrow{GB}\times\vec{B}_R= (F_0-B_R)R\,\vec{k} = \vec{0} \qquad (3)\\ & \overrightarrow{GC}\times\vec{F} = -F_0R\,\vec{k}\\ & \overrightarrow{GB}\times\vec{B}_R = B_RR\,\vec{k} \end{array}$

Estos momentos son fáciles de calcular porque los vectores implicados en los productos vectoriales son mutuamente perpendiculares.

Resolviendo las ecuaciones obtenemos las fuerzas

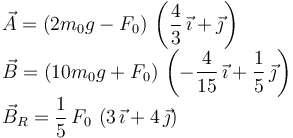
$\begin{array}{l} \vec{A} = (2m_0g-F_0)\,\left(\dfrac{4}{3}\,\vec{\imath} + \vec{\jmath}\right)\\ \vec{B} = (10m_0g+F_0)\,\left(-\dfrac{4}{15}\,\vec{\imath} + \dfrac{1}{5}\,\vec{\jmath}\right)\\ \vec{B}_R = \dfrac{1}{5}\,F_0\,\left(3\,\vec{\imath} + 4\,\vec{\jmath}\right) \end{array}$

Valor de $F 0$ para que el disco empiece a rotar

Esto ocurrirá cuando el disco se separe en el punto $A$ . Para que esto suceda debe anularse la fuerza vincular en $A$

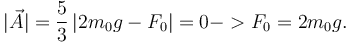
$|\vec{A}| = \dfrac{5}{3}\,|2m_0g-F_0|=0 -> F_0 = 2m_0g.$

Condición sobre $μ$ para que el disco no deslice

Cuando $F 0 = 2 m 0 g$ las fuerzas en $B$ son

$\begin{array}{l} \vec{B} = \dfrac{4}{5}m_0g\,\left(-4\,\vec{\imath} + 3\,\vec{\jmath}\right)\\ \vec{B}_R = \dfrac{2}{5}m_0g \,(3\,\vec{\imath}+ 4\,\vec{\jmath}) \end{array}$

La condición de no deslizamiento en $B$ es

$|\vec{B}_R|> \mu|\vec{B}| \to \mu>1/2$

Disco apoyado en dos esquinas (Ene. 2021 G.I.C.)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES