Muelle forzado
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 25: | Línea 25: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \omega_0 = \sqrt{\dfrac{k}{m}} = 11.5\,\mathrm{rad/s}. \qquad\qquad(3) | + | \omega_0 = \sqrt{\dfrac{k}{m}} = 11.5\,\mathrm{rad/s}. \qquad\qquad(3) |
</math> | </math> | ||
</center> | </center> | ||
última version al 12:10 3 may 2020
1 Enunciado
Una pesa de 1.50 kg está suspendida de un muelle con una constante elástica 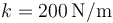 . Una fuerza sinusoidal con una magnitud de 50.0 N excita el sistema. El factor de rozamiento es
. Una fuerza sinusoidal con una magnitud de 50.0 N excita el sistema. El factor de rozamiento es 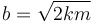 ¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m?
¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m?
2 Solución
Cuando un muelle está sometido a una fuerza externa periódica de frecuencia ωe, después de un período transitorio, oscila con una frecuencia igual a la de la fuerza externa
x(t) = Acos(ωet + Φ)
La amplitud de la oscilación es
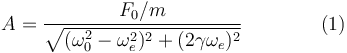
Aquí, F0 es la amplitud de la fuerza externa, 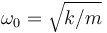 es la frecuencia propia del muelle y γ = b / 2m es el parámetro de rozamiento.
Vamos a introducir un cambio de variable y escribir la frecuencia de excitación que buscamos, ωe, de la forma
es la frecuencia propia del muelle y γ = b / 2m es el parámetro de rozamiento.
Vamos a introducir un cambio de variable y escribir la frecuencia de excitación que buscamos, ωe, de la forma

Vamos a buscar una ecuación para el número λ.
La frecuencia propia del oscilador es
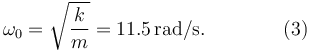
El parámetro de rozamiento es
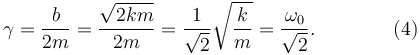
Introduciendo el cambio de variable (2) en la expresión (1) tenemos
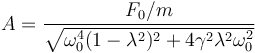
Ahora usamos la expresión (4)
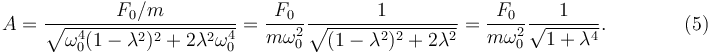
Ahora podemos despejar λ
![1+\lambda^4 = \left(\dfrac{F_0}{m\omega_0^2A}\right)^2
\Longrightarrow
\lambda = \left[ \left(\dfrac{F_0}{m\omega_0^2A}\right)^2 -1\right]^{1/4}. \qquad\qquad (6)](/wiki/images/math/b/f/5/bf5e7f173e95be2ddcaa84d03b66796a.png)
Sustituyendo los valores numéricos tenemos
Y la frecuencia pedida es