Problemas de dinámica del sólido rígido (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Momento de inercia de un sistema de partículas== Se tiene un sólido formado por ocho partículas de masa <math>m</math> situadas en los vértices de un cubo de arista <math>…') |
(→Momento de inercia de sólidos esféricos) |
||
| Línea 18: | Línea 18: | ||
[[Momento de inercia de sólidos esféricos|Solución]] | [[Momento de inercia de sólidos esféricos|Solución]] | ||
| + | |||
| + | ==Momento de inercia de sólidos cilíndricos== | ||
| + | Halle los siguientes momentos de inercia de sólidos de densidad homogénea: | ||
| + | |||
| + | # Una superficie cilíndrica hueca, de masa ''M'', radio ''R'' y altura ''H''. | ||
| + | # Un cilindro macizo, de masa ''M'', radio ''R'' y altura ''H''. | ||
| + | # Una corona cilíndrica de masa ''M'', radio interior ''R''<sub>1</sub> y exterior ''R''<sub>2</sub>, con altura ''H'' | ||
| + | |||
| + | En todos los casos, el momento de inercia debe hallarse respecto al eje del cilindro. | ||
| + | |||
| + | [[Momento de inercia de sólidos cilíndricos|Solución]] | ||
Revisión de 15:34 16 dic 2019
1 Momento de inercia de un sistema de partículas
Se tiene un sólido formado por ocho partículas de masa m situadas en los vértices de un cubo de arista b.
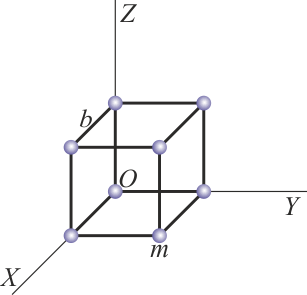
Halle el momento de inercia del cubo respecto a los siguientes ejes:
- Uno perpendicular a una cara y que pase por el centro del cubo.
- Uno que pase por dos vértices opuestos.
- Uno que pase por los centros de dos aristas opuestas.
- Uno que pase por una arista
2 Momento de inercia de sólidos esféricos
Calcule el momento de inercia de una esfera maciza, de masa M y radio R alrededor de de un eje que pasa por su centro.
A partir del resultado anterior, halle el momento de inercia de una esfera hueca, de masa M, radio interior R1 y exterior R2 respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado cuando la corona se reduce a una superficie esférica de radio R?
3 Momento de inercia de sólidos cilíndricos
Halle los siguientes momentos de inercia de sólidos de densidad homogénea:
- Una superficie cilíndrica hueca, de masa M, radio R y altura H.
- Un cilindro macizo, de masa M, radio R y altura H.
- Una corona cilíndrica de masa M, radio interior R1 y exterior R2, con altura H
En todos los casos, el momento de inercia debe hallarse respecto al eje del cilindro.





