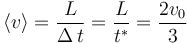No Boletín - Celeridad media (Ex.Oct/18)
De Laplace
| Línea 5: | Línea 5: | ||
¿Cuál es la celeridad media de la partícula en el intervalo de tiempo transcurrido entre el instante inicial y el instante en el que se detiene? | ¿Cuál es la celeridad media de la partícula en el intervalo de tiempo transcurrido entre el instante inicial y el instante en el que se detiene? | ||
| - | == | + | ==Posición y velocidad en función del tiempo== |
| + | Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir: | ||
| + | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{d}\vec{r}=\vec{v}\,\mathrm{d}t \,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=-C\, t\,\vec{\imath}\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{d}\vec{v}=-C\, t\,\mathrm{d}t\,\vec{\imath}</math></center> | ||
| + | |||
| + | Conocemos la velocidad inicial de la partícula, y podemos suponer sin pérdida de generalidad que su posición inicial coincide con el origen de coordenadas: | ||
| + | <center><math>\vec{r}(0)=\vec{0}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{v}(0)=v_0\,\vec{\imath}</math></center> | ||
| + | |||
| + | Por tanto, determinar la velocidad y la posición de la partícula en función del tiempo se reduce a integrar su aceleración una y dos veces, respectivamente, entre el instante inicial y el instante genérico <math>t\,</math>: | ||
| + | <center><math> | ||
| + | \begin{array}{lll} \displaystyle\int_{\vec{v}(0)}^{\vec{v}(t)}\!\mathrm{d}\vec{v}=-C\left(\displaystyle\int_{0}^{t}\!t\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}(t)=\vec{v}(0)-\displaystyle\frac{Ct^2}{2}\,\vec{\imath}=\left(v_0-\displaystyle\frac{Ct^2}{2}\right)\,\vec{\imath} \\ \\ | ||
| + | \displaystyle\int_{\vec{r}(0)}^{\vec{r}(t)}\!\mathrm{d}\vec{r}=\left[v_0\left(\displaystyle\int_{0}^{t}\,\mathrm{d}t\right)-\frac{C}{2}\left(\displaystyle\int_{0}^{t}\!t^2\,\mathrm{d}t\right)\right]\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}(t)=\vec{r}(0)+\left[\,v_0\,t-\displaystyle\frac{Ct^3}{6}\,\right]\,\vec{\imath}=\left[\,v_0\,t-\displaystyle\frac{Ct^3}{6}\,\right]\,\vec{\imath}\end{array} | ||
| + | </math></center> | ||
| + | |||
| + | ==Instante en el que la partícula se detiene== | ||
| + | Igualando a cero la velocidad de la partícula, determinamos en qué instante (<math>t=t^{*}\,</math>) se detiene: | ||
| + | <center><math> | ||
| + | \vec{v}(t^{*})=\vec{0} \,\,\,\,\,\longrightarrow\,\,\,\,\, \left(v_0-\displaystyle\frac{C(t^{*})^2}{2}\right)\,\vec{\imath}=\vec{0}\,\,\,\,\,\longrightarrow\,\,\,\,\,v_0-\displaystyle\frac{C(t^{*})^2}{2}=0\,\,\,\,\,\longrightarrow\,\,\,\,\,t^{*}=\displaystyle\sqrt{\frac{2v_0}{C}} | ||
| + | </math></center> | ||
| + | |||
| + | ==Celeridad media en el intervalo de tiempo solicitado== | ||
| + | Nótese que <math>v_x(t)=v_0-\displaystyle\frac{C(t^)^2}{2}\,</math> es positiva en el intervalo de tiempo <math>0\leq t<t^{*}\,</math>, lo cual implica que la partícula se mueve en el sentido positivo del eje <math>\,OX\,</math> durante todo el intervalo de interés, y esto nos permite identificar la distancia <math>L\,</math> recorrida por la partícula durante dicho intervalo como el incremento de su coordenada <math>\Delta\, x\,</math>: | ||
| + | <center><math> | ||
| + | L=\Delta\, x=x(t^{*})-x(0)=v_0\,t^{*}-\displaystyle\frac{C(t^{*})^3}{6}=v_0\displaystyle\sqrt{\frac{2v_0}{C}}-\displaystyle\frac{C}{6}\displaystyle\frac{2v_0}{C}\displaystyle\sqrt{\frac{2v_0}{C}}=\frac{2v_0}{3}\sqrt{\frac{2v_0}{C}} | ||
| + | </math></center> | ||
| + | |||
| + | Finalmente, la celeridad media de la partícula en el intervalo de tiempo de interés viene dada por el siguiente cociente: | ||
| + | <center><math> | ||
| + | \left\langle v\right\rangle = \frac{L}{\Delta\, t}=\frac{L}{t^{*}}=\displaystyle\frac{2v_0}{3} | ||
| + | </math></center> | ||
[[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)]] | ||
Revisión de 19:21 25 mar 2019
Contenido |
1 Enunciado
Una partícula, que se mueve a lo largo del eje  , tiene en el instante inicial
, tiene en el instante inicial 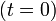 una velocidad
una velocidad 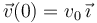 (donde
(donde 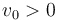 ) y sufre una desaceleración creciente en el tiempo, dada por la función
) y sufre una desaceleración creciente en el tiempo, dada por la función 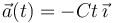 (donde
(donde
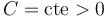 ), hasta que finalmente se detiene.
), hasta que finalmente se detiene.
¿Cuál es la celeridad media de la partícula en el intervalo de tiempo transcurrido entre el instante inicial y el instante en el que se detiene?
2 Posición y velocidad en función del tiempo
Conforme a las definiciones de velocidad instantánea y aceleración instantánea, podemos escribir:
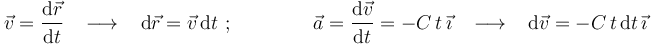
Conocemos la velocidad inicial de la partícula, y podemos suponer sin pérdida de generalidad que su posición inicial coincide con el origen de coordenadas:

Por tanto, determinar la velocidad y la posición de la partícula en función del tiempo se reduce a integrar su aceleración una y dos veces, respectivamente, entre el instante inicial y el instante genérico  :
:
![\begin{array}{lll} \displaystyle\int_{\vec{v}(0)}^{\vec{v}(t)}\!\mathrm{d}\vec{v}=-C\left(\displaystyle\int_{0}^{t}\!t\,\mathrm{d}t\right)\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{v}(t)=\vec{v}(0)-\displaystyle\frac{Ct^2}{2}\,\vec{\imath}=\left(v_0-\displaystyle\frac{Ct^2}{2}\right)\,\vec{\imath} \\ \\
\displaystyle\int_{\vec{r}(0)}^{\vec{r}(t)}\!\mathrm{d}\vec{r}=\left[v_0\left(\displaystyle\int_{0}^{t}\,\mathrm{d}t\right)-\frac{C}{2}\left(\displaystyle\int_{0}^{t}\!t^2\,\mathrm{d}t\right)\right]\vec{\imath} & \,\,\,\,\,\longrightarrow\,\,\,\,\, & \vec{r}(t)=\vec{r}(0)+\left[\,v_0\,t-\displaystyle\frac{Ct^3}{6}\,\right]\,\vec{\imath}=\left[\,v_0\,t-\displaystyle\frac{Ct^3}{6}\,\right]\,\vec{\imath}\end{array}](/wiki/images/math/1/1/9/1194a2ce564b0291b9142683e4970eb7.png)
3 Instante en el que la partícula se detiene
Igualando a cero la velocidad de la partícula, determinamos en qué instante (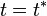 ) se detiene:
) se detiene:
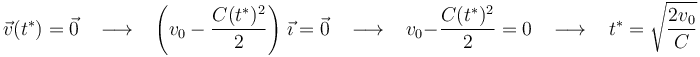
4 Celeridad media en el intervalo de tiempo solicitado
Nótese que No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): v_x(t)=v_0-\displaystyle\frac{C(t^)^2}{2}\,
es positiva en el intervalo de tiempo, lo cual implica que la partícula se mueve en el sentido positivo del eje
durante todo el intervalo de interés, y esto nos permite identificar la distancia
recorrida por la partícula durante dicho intervalo como el incremento de su coordenada
:
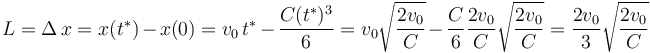
Finalmente, la celeridad media de la partícula en el intervalo de tiempo de interés viene dada por el siguiente cociente: