Primera convocatoria 2017/18 (F2GIA)

De Laplace

Revisión de 13:25 8 jul 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Campo eléctrico de distribución volumétrica de carga con simetría radial) ← Edición más antigua		Revisión de 13:26 8 jul 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Campo eléctrico de distribución volumétrica de carga con simetría radial) Edición más nueva →
Línea 15:		Línea 15:
	sistema.		sistema.
-	# ?`C\'{o}mo es la	+	# ?`C\'{o}mo es la componente radial del campo el\'{e}ctrico <math>E(r)</math> creado por la distribuci\'{o}n descrita, tanto dentro como fuera de la esfera
-	componente radial del campo el\'{e}ctrico <math>E(r)</math> creado por la	+
-	distribuci\'{o}n descrita, tanto dentro como fuera de la esfera	+
	<math>\tau_0</math>?		<math>\tau_0</math>?
-	# ¿Cómo es el potencial electrostático creado por la distribución	+	# ¿Cómo es el potencial electrostático creado por la distribución en el exterior de <math>\tau_0</math>? ¿Cuánto vale el potencial en el centro <math>O</math>?
-	en el exterior de <math>\tau_0</math>? ¿Cuánto vale el potencial en el centro <math>O</math>?	+
	por lo que el campo el\'{e}ctrico en el entorno de la esfera		por lo que el campo el\'{e}ctrico en el entorno de la esfera
	$\tau_0$ presenta simetr\'{\i}a radial $\vec{E}(\vec{r})=E(r)\es		$\tau_0$ presenta simetr\'{\i}a radial $\vec{E}(\vec{r})=E(r)\es
	\vec{u}_r$, con centro en $O$; es decir,		\vec{u}_r$, con centro en $O$; es decir,
	$\overrightarrow{OP}=\vec{r}=r\es \vec{u}_r$		$\overrightarrow{OP}=\vec{r}=r\es \vec{u}_r$

---

Revisión de 13:26 8 jul 2018

1 Fuerza eléctrica en sistema de cuatro cargas puntuales

Dos cargas eléctricas puntuales idénticas de valor Q, ocupan sendos puntos A y C que, en un sistema de referencia $OXYZ$, tienen coordenadas cartesianas A(a,0,0) y C( − a,0,0). Otras dos cargas idénticas entre sí y de valor q, ocupan los puntos B y D del eje OY, cuyas coordenadas cartesianas son B(0,b,0) y D(0, − b,0). La geometría

del sistema es tal que la distancia que separa dos carta contiguas es

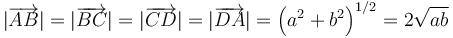
No existen más cargas eléctricas, a parte de las cuatro que constituyen el sistema descrito.

1. ¿Qué relación deben verificar la cantidades de Q y q de las respectivas cargas puntuales descritas en el sistema para que la fuerza eléctrica resultante que actúa sobre la carga que ocupa el punto A sea nula, ?
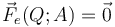2. En las condiciones del apartado anterior, ¿cómo es la fuerza eléctrica resultante que actúa sobre cada una de las otras tres cargas?

2 Campo eléctrico de distribución volumétrica de carga con simetría radial

En una esfera τ₀ de radio R₀ y centro en O, existe una distribuci\'{o}n no uniforme de carga eléctrica negativa descrita por una densidad volum\'{e}trica radial ρ_e(r), respecto del punto O, de manera que r es la distancia desde dicho centro al punto P donde se mide la densidad de carga. Dicha distribuci\'{o}n es tal que si consideramos una regi\'{o}n esf\'{e}rica τ con centro en O y radio 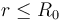, la cantidad parcial de carga contenida en τ es 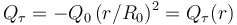. No hay m\'{a}s cargas en el sistema.

1.  ?`C\'{o}mo es la componente radial del campo el\'{e}ctrico E(r) creado por la distribuci\'{o}n descrita, tanto dentro como fuera de la esfera

τ₀?

1. ¿Cómo es el potencial electrostático creado por la distribución en el exterior de τ₀? ¿Cuánto vale el potencial en el centro O?

por lo que el campo el\'{e}ctrico en el entorno de la esfera

$\tau_0$ presenta simetr\'{\i}a radial $\vec{E}(\vec{r})=E(r)\es \vec{u}_r$, con centro en $O$; es decir, $\overrightarrow{OP}=\vec{r}=r\es \vec{u}_r$