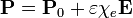Medio polarizado entre dos placas
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | + | Entre dos placas metálicas planas y paralelas, de sección <math>S</math> y separadas una distancia <math>a</math>, se encuentra un dieléctrico que presenta polarización remanente, de forma que en él | |
| - | <center><math>\mathbf{P} = | + | <center><math>\mathbf{P} = \mathbf{P}_0</math></center> |
| - | + | siendo <math>\mathbf{P}_0</math> un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante. | |
| - | # | + | # Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste? |
| - | # | + | # Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica? |
| - | + | # Calcule cómo cambian los resultados si la polarización del dieléctrico no es constante, sino que depende del campo como | |
| + | |||
| + | <center><math>\mathbf{P} = \mathbf{P}_0 +\varepsilon\chi_e\mathbf{E}</math></center> | ||
==Solución== | ==Solución== | ||
Revisión de 18:27 8 may 2010
Contenido |
1 Enunciado
Entre dos placas metálicas planas y paralelas, de sección S y separadas una distancia a, se encuentra un dieléctrico que presenta polarización remanente, de forma que en él

siendo 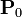 un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante.
un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante.
- Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste?
- Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica?
- Calcule cómo cambian los resultados si la polarización del dieléctrico no es constante, sino que depende del campo como