Partícula en anilla giratoria
De Laplace
| Línea 30: | Línea 30: | ||
Este vínculo es liso, bilateral, reónomo (pues depende del tiempo) y geométrico. Al ser geométrico, es también holónomo. | Este vínculo es liso, bilateral, reónomo (pues depende del tiempo) y geométrico. Al ser geométrico, es también holónomo. | ||
| + | ==Ecuaciones de movimiento== | ||
| + | ===Coordenadas=== | ||
| + | Para describir el movimiento emplearemos la base de cilíndricas y parametrizamos la ecuación de la curva como | ||
| + | |||
| + | <center><math>\rho = b\,\mathrm{sen}(\phi)\qquad\qquad \theta=\Omega t\qquad\qquad z = -b\cos(\phi)</math></center> | ||
| + | |||
| + | siendo <math>\phi</math> el ángulo con la vertical descendente. En realidad, esto equivale a usar coordenadas esféricas, pero lo haremos así para aprovechar las fórmulas de coordenadas cilíndricas, más fáciles de recordar. | ||
| + | |||
| + | Empleando la abreviatura, que usaremos en lo sucesivo | ||
| + | |||
| + | <center><math>C=\cos(\phi)\qquad\qquad S=\mathrm{sen}(\phi)</math></center> | ||
| + | |||
| + | estas coordenadas se escriben | ||
| + | |||
| + | <center><math>\rho = b\,S\qquad\qquad \theta=\Omega t\qquad\qquad z = -b\,C</math></center> | ||
| + | |||
| + | Las derivadas respecto al tiempo valen, por la regla de la cadena | ||
| + | |||
| + | <center><math>\dot{\rho} = b\,\dot{\phi}\,C\qquad\qquad \dot{\theta}=\Omega \qquad\qquad \dot{z} = b\,\dot{\phi}\,S</math></center> | ||
| + | |||
| + | y las segundas derivadas | ||
| + | |||
| + | <center><math>\ddot{\rho} = b(\ddot{\phi}\,C-\dot{\phi}^2S)\qquad\qquad \ddot{\theta}=0 \qquad\qquad \ddot{z} = b(\ddot{\phi}\,S+\dot{\phi}^2\,C)</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
==Puntos de equilibrio== | ==Puntos de equilibrio== | ||
===Posiciones de equilibrio=== | ===Posiciones de equilibrio=== | ||
Revisión de 13:27 2 dic 2017
Contenido |
1 Enunciado
Una pequeña anilla de masa m está ensartada sin rozamiento en un aro circular de masa M y radio b situado verticalmente que puede girar en torno a un diámetro vertical. Suponga que este aro se hace girar con velocidad angular constante Ω alrededor de este diámetro.
- Escriba la ecuación del vínculo sobre la partícula. ¿De qué tipo es?
- Determine la posición de los posibles puntos de equilibrio en la vertical, así como la estabilidad de éstos, en función del valor de Ω.
- Suponga ahora que entre la anilla y el aro existe un coeficiente de rozamiento seco μ, ¿cómo queda en ese caso la ecuación de movimiento para la anilla? Para un valor de Ω dado, ¿cuál es en ese caso el rango de posiciones verticales de equilibrio?
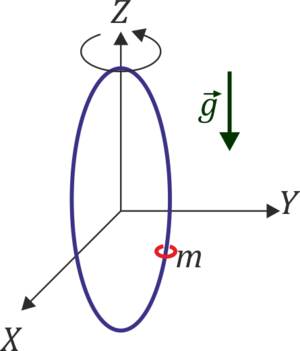
2 Ecuación del vínculo
La partícula está obligada a moverse sobre una línea, la cual la podemos considerar como una intersección de dos superficies:
- Una esfera de radio b
- o, en cilíndricas,
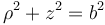
- o, en esféricas,
- Un plano giratorio. Este plano fija la coordenada θ de cilíndricas, en
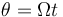
- (que sería
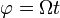en esféricas). En cartesianas, sería
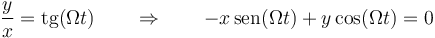
Este vínculo es liso, bilateral, reónomo (pues depende del tiempo) y geométrico. Al ser geométrico, es también holónomo.
3 Ecuaciones de movimiento
3.1 Coordenadas
Para describir el movimiento emplearemos la base de cilíndricas y parametrizamos la ecuación de la curva como
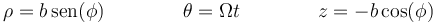
siendo φ el ángulo con la vertical descendente. En realidad, esto equivale a usar coordenadas esféricas, pero lo haremos así para aprovechar las fórmulas de coordenadas cilíndricas, más fáciles de recordar.
Empleando la abreviatura, que usaremos en lo sucesivo
estas coordenadas se escriben
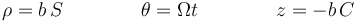
Las derivadas respecto al tiempo valen, por la regla de la cadena
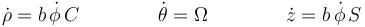
y las segundas derivadas
4 Puntos de equilibrio
4.1 Posiciones de equilibrio
Si el aro no girara, habría solo dos posiciones de equilibrio, una en el punto más bajo y otra en el punto más alto. La primera sería estable y la segunda inestable.
La rotación del aro introduce nuevas posiciones de equilibrio. Podemos visualizarlo imaginando la acción de una fuerza centrífuga que apunta hacia el exterior, posibilitando que la anilla se quede estacionaria a una cierta altura.
Hay que señalar que en ese caso, estas posiciones serían estacionarias respecto al aro, pero no respecto a un observador exterior, el cual vería la anilla dar vueltas alrededor del eje, como el resto del aro en que se halla ensartada.
