Disco en varilla horizontal (CMR)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un disco de radio R (“sólido 2”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 0”). Este eje es…') |
|||
| Línea 9: | Línea 9: | ||
# Halle las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math>. | # Halle las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math>. | ||
# Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3). | # Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3). | ||
| + | [[Categoría:Problemas de cinemática del movimiento relativo (CMR)]] | ||
Revisión de 15:06 10 nov 2017
Enunciado
Un disco de radio R (“sólido 2”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 0”). Este eje está montado sobre un soporte vertical fijo de altura R. El disco rueda sin deslizar sobre la superficie horizontal z = 0 (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje OX0 es a lo largo de la barra horizontal y OZ0 = OZ1 en todo momento. Sea (t) el ángulo que el eje OX0 forma con el OX1. En un instante dado 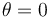 ,
, 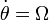 ,
, 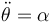 .
.
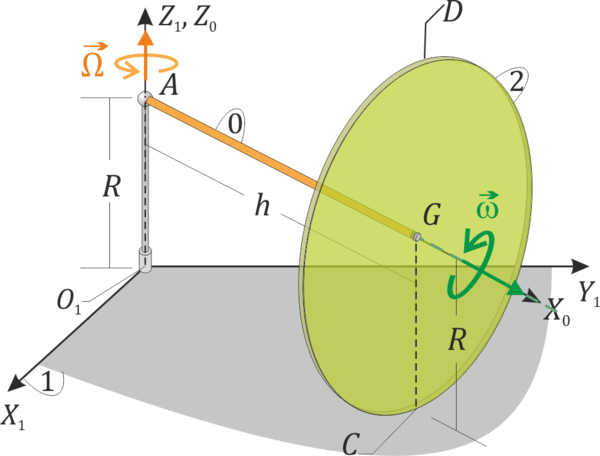
Para ese instante:
- Determine los vectores
 ,
,  y
y  .
.
- Halle la posición de los ejes instantáneos de rotación en los movimientos {01}, {20} y {21}.
- Calcule las velocidades en el movimiento {21} y el {20} del punto C de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco.
- Halle las aceleraciones angulares
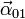 ,
, 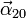 y
y 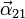 .
.
- Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3).





