Problemas de cinemática del movimiento relativo (CMR)
De Laplace
(→Peonza rodante) |
|||
| Línea 1: | Línea 1: | ||
| - | ==Peonza rodante== | + | ==[[Peonza rodante (CMR)|Peonza rodante]]== |
Una peonza está formada por una varilla de longitud <math>\ell=20\,cm</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez <math>v_0=48\,\mathrm{cm}/\mathrm{s}</math>. El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula. | Una peonza está formada por una varilla de longitud <math>\ell=20\,cm</math> ensartada en un disco de radio <math>R=15\,\mathrm{cm}</math>. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez <math>v_0=48\,\mathrm{cm}/\mathrm{s}</math>. El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula. | ||
| Línea 9: | Línea 9: | ||
# La aceleración angular del sólido. | # La aceleración angular del sólido. | ||
# La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido. | # La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido. | ||
| + | |||
| + | ==[[Disco en varilla horizontal (CMR)|Disco en varilla horizontal]]== | ||
| + | Un disco de radio R (“sólido 2”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 0”). Este eje está montado sobre un soporte vertical fijo de altura R. El disco rueda sin deslizar sobre la superficie horizontal <math>z=0</math> (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje <math>OX_0</math> es a lo largo de la barra horizontal y <math>OZ_0=OZ_1</math> en todo momento. Sea <math>θ(t)</math> el ángulo que el eje <math>OX_0</math> forma con el <math>OX_1</math>. En un instante dado <math>\theta=0</math>,<math>\dot{\theta}=\Omega</math>,<math>\ddot{\theta}=\alpha</math>. | ||
| + | |||
| + | <center>[[Archivo:disco-varilla-horizontal.png|800px]]</center> | ||
| + | Para ese instante: | ||
| + | # Determine los vectores <math>\vec{\omega}_{01}</math>, <math>\vec{\omega}_{20}</math> y <math>\vec{\omega}_{21}</math>. | ||
| + | # Halle la posición de los ejes instantáneos de rotación en los movimientos {01}, {20} y {21}. | ||
| + | # Calcule las velocidades en el movimiento {21} y el {20} del punto C de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco. | ||
| + | # Halle las aceleraciones angulares <math>\vec{\alpha}_{01}</math>, <math>\vec{\alpha}_{20}</math> y <math>\vec{\alpha}_{21}</math>. | ||
| + | # Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3). | ||
Revisión de 19:30 7 nov 2017
1 Peonza rodante
Una peonza está formada por una varilla de longitud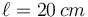 
ensartada en un disco de radio 
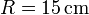. Esta peonza se mueve de forma que el extremo O de la varilla está inmóvil mientras el centro G del disco describe un movimiento circular uniforme alrededor del eje OZ con rapidez 
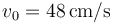. El disco rueda sin deslizar sobre el plano OXY, de manera que en todo instante la velocidad del punto de contacto A es nula.
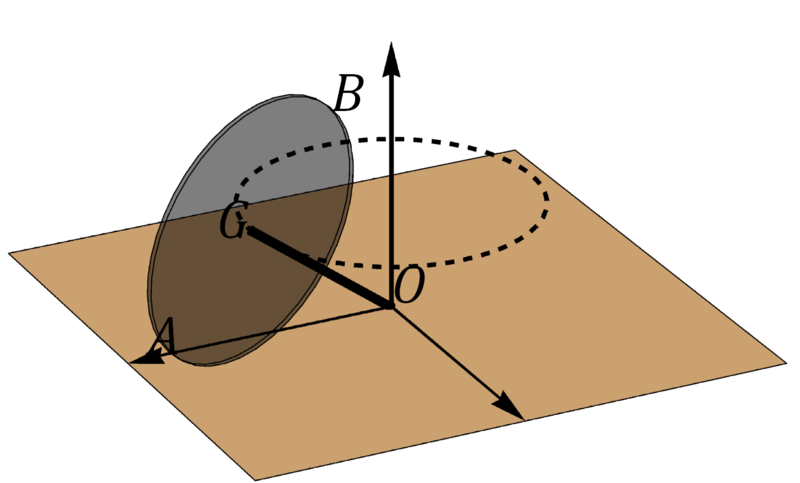
Para este movimiento, determine, en el instante en que A se encuentra sobre el eje OX:
- La velocidad angular del sólido.
- La velocidad del punto B, diametralmente opuesto a A, y del punto P situado en
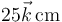, considerado como punto del sólido.
- La aceleración angular del sólido.
- La aceleración de los puntos A, G, B, O y P, considerados como puntos del sólido.
2 Disco en varilla horizontal
Un disco de radio R (“sólido 2”) se encuentra ensartado mediante un rodamiento sin fricción en un eje horizontal de longitud h (“sólido 0”). Este eje está montado sobre un soporte vertical fijo de altura R. El disco rueda sin deslizar sobre la superficie horizontal z = 0 (“sólido 1”). Consideramos tres sistemas de referencia. Uno fijo en el suelo, uno ligado al disco, y uno intermedio en el que el eje OX0 es a lo largo de la barra horizontal y OZ0 = OZ1 en todo momento. Sea (t) el ángulo que el eje OX0 forma con el OX1. En un instante dado θ = 0,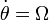
,
.
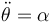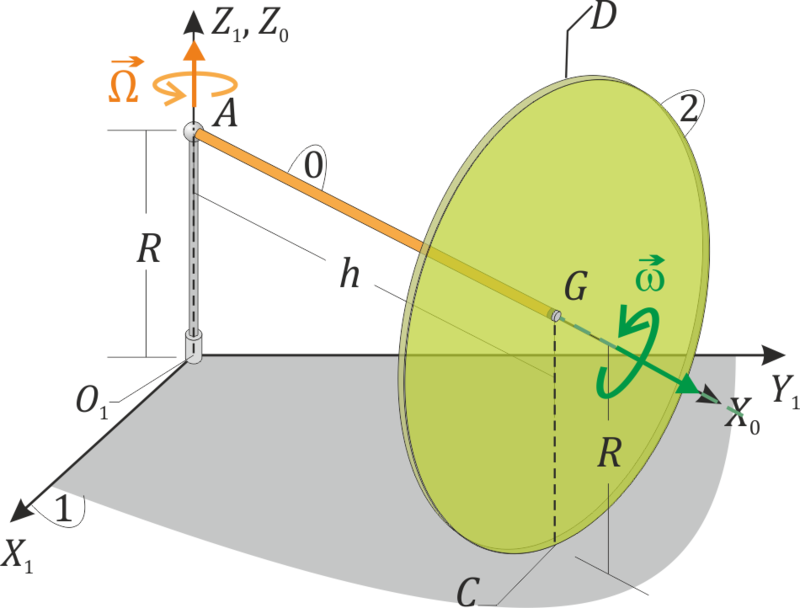
Para ese instante:
- Determine los vectores
, 
y 
.
- Halle la posición de los ejes instantáneos de rotación en los movimientos {01}, {20} y {21}.
- Calcule las velocidades en el movimiento {21} y el {20} del punto C de contacto del disco con el suelo; del G, centro del disco, y de D, el punto más alto del disco.
- Halle las aceleraciones angulares
, 
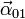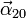y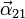 
.
- Calcule las aceleraciones en los movimientos {21} y {20} de los puntos C, G y D del apartado (3).
