Entrar Página Discusión Historial Go to the site toolbox

Movimiento expresado en polares

De Laplace

(Diferencias entre revisiones)
Línea 47: Línea 47:
<center><math>\vec{a}=\frac{23\vec{u}_\rho-36\vec{u}_\theta}{4t^3}</math></center>
<center><math>\vec{a}=\frac{23\vec{u}_\rho-36\vec{u}_\theta}{4t^3}</math></center>
 +
 +
==Triedro de Frenet==
 +
===Vector tangente===
 +
Es el paralelo a la velocidad
 +
 +
<center><math>\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\frac{4}{5}\vec{u}_\rho+\frac{3}{5}\vec{u}_\theta</math></center>
 +
 +
===Vector binormal===
 +
Es el perpendicular al plano definido por la velocidad de la aceleración, es decir, en la dirección de <math>\vec{k}</math>, con el sentido dado por el producto vectorial.
[[Categoría:Problemas de cinemática tridimensional (GIE)]]
[[Categoría:Problemas de cinemática tridimensional (GIE)]]

Revisión de 20:38 10 oct 2017

Contenido

1 Enunciado

Una partícula se mueve de forma que en el SI sus coordenadas polares valen, en todo instante t > 0,

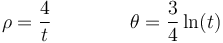
\rho=\frac{4}{t}\qquad\qquad\theta=\frac{3}{4}\ln(t)

Para el instante t=1\,\mathrm{s} halle…

  1. Velocidad y rapidez
  2. Vector aceleración y componentes intrínsecas de la aceleración.
  3. Triedro de Frenet.
  4. Radio de curvatura y centro de curvatura.

2 Velocidad y rapidez

La velocidad de una partícula, expresada en coordenadas polares, viene dada por

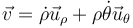
\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta

donde, en este caso,

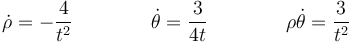
\dot{\rho}=-\frac{4}{t^2}\qquad\qquad\dot{\theta}=\frac{3}{4t}\qquad\qquad \rho\dot{\theta}=\frac{3}{t^2}

lo que nos da la velocidad

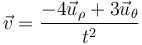
\vec{v}=\frac{-4\vec{u}_\rho+3\vec{u}_{\theta}}{t^2}

y la rapidez

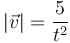
|\vec{v}|=\frac{5}{t^2}

3 Aceleración

Expresada en polares, la aceleración es

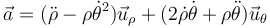
\vec{a}=(\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho + (2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{u}_\theta

con

\ddot{\rho}=\frac{8}{t^3}\qquad\qquad\ddot{\theta}=-\frac{3}{4t^2}

Nos queda la aceleración radial

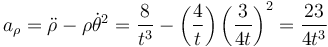
a_\rho=\ddot{\rho}-\rho\dot{\theta}^2=\frac{8}{t^3}-\left(\frac{4}{t}\right)\left(\frac{3}{4t}\right)^2=\frac{23}{4t^3}

y la acimutal o lateral

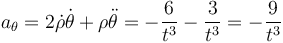
a_\theta=2\dot{\rho}\dot{\theta}+\rho\ddot{\theta}=-\frac{6}{t^3}-\frac{3}{t^3}=-\frac{9}{t^3}

El vector aceleración es entonces

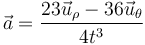
\vec{a}=\frac{23\vec{u}_\rho-36\vec{u}_\theta}{4t^3}

4 Triedro de Frenet

4.1 Vector tangente

Es el paralelo a la velocidad

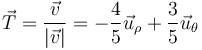
\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\frac{4}{5}\vec{u}_\rho+\frac{3}{5}\vec{u}_\theta

4.2 Vector binormal

Es el perpendicular al plano definido por la velocidad de la aceleración, es decir, en la dirección de \vec{k}, con el sentido dado por el producto vectorial.

Obtenido de "http://tesla.us.es/wiki/index.php/Movimiento_expresado_en_polares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace