Movimiento expresado en polares
De Laplace
Contenido |
1 Enunciado
Una partícula se mueve de forma que en el SI sus coordenadas polares valen, en todo instante t > 0,
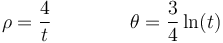
Para el instante  halle…
halle…
- Velocidad y rapidez
- Vector aceleración y componentes intrínsecas de la aceleración.
- Triedro de Frenet.
- Radio de curvatura y centro de curvatura.
2 Velocidad y rapidez
La velocidad de una partícula, expresada en coordenadas polares, viene dada por
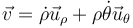
donde, en este caso,
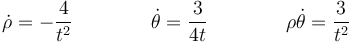
lo que nos da la velocidad
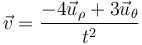
y la rapidez
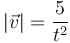
3 Aceleración
3.1 Vector aceleración
Expresada en polares, la aceleración es
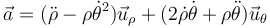
con

Nos queda la aceleración radial
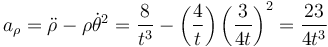
y la acimutal o lateral
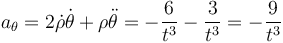
El vector aceleración es entonces
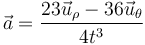
3.2 Aceleración tangencial
En su forma escalar, la componente tangencial la da la derivada de la rapidez respecto al tiempo
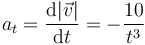
En su forma vectorial, multiplicamos esta cantidad por el vector tangente, unitario paralelo a la velocidad
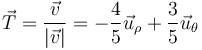
y queda
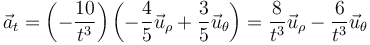
3.3 Aceleración normal
El vector aceleración normal lo obtenemos mediante la substracción vectorial
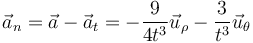
y su forma escalar hallando el módulo de este vector
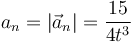
También puede calcularse mediante el teorema de Pitágoras
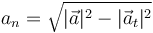
4 Triedro de Frenet
4.1 Vector tangente
Ya lo hemos obtenido como el unitario paralelo a la velocidad
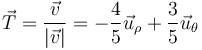
4.2 Vector binormal
Es el perpendicular al plano definido por la velocidad de la aceleración, es decir, en la dirección de  , con el sentido dado por el producto vectorial.
, con el sentido dado por el producto vectorial.
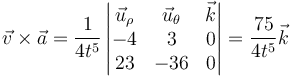
Normalizando este vector queda
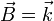
4.3 Vector normal
Completamos el triedro con ayuda del producto vectorial
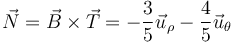
También podemos hallarlo normalizando la aceleración normal
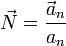
5 Radio y centro de curvatura
Obtenemos el radio a partir de la aceleración normal y la rapidez
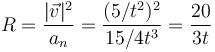
Por último, el centro de curvatura, lo hallamos como
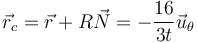
Hay que indicar que este vector 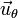 es el referido a la posición de la partícula, no al punto
es el referido a la posición de la partícula, no al punto 





