Anilla ensartada en dos varillas rotatorias (GIE)

De Laplace

Revisión de 13:34 19 sep 2017 (ver código fuente) Antonio (Discusión | contribuciones) ← Edición más antigua		Revisión de 13:35 19 sep 2017 (ver código fuente) Antonio (Discusión | contribuciones) Edición más nueva →
Línea 1:		Línea 1:
	==Enunciado==		==Enunciado==
	Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos <math>O</math> y <math>A</math> que distan una cantidad <math>b</math>. Las dos barras giran en sentido positivo, la de O con velocidad angular 2Ω y la de A con velocidad angular Ω. Inicialmente la barra de O se halla situada horizontalmente y la de A verticalmente.<center>		Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos <math>O</math> y <math>A</math> que distan una cantidad <math>b</math>. Las dos barras giran en sentido positivo, la de O con velocidad angular 2Ω y la de A con velocidad angular Ω. Inicialmente la barra de O se halla situada horizontalmente y la de A verticalmente.<center>
-	[[Archivo:barras-anilla.png]]</center>	+	[[Archivo:barras-anilla.png|300px]]</center>
	# Determine la posición, velocidad y aceleración de la anilla como función del tiempo.		# Determine la posición, velocidad y aceleración de la anilla como función del tiempo.
	# Para el instante en que <math>\mathrm{tg}⁡(\Omega t)=1/2</math> halle		# Para el instante en que <math>\mathrm{tg}⁡(\Omega t)=1/2</math> halle

---

Revisión de 13:35 19 sep 2017

Contenido 1 Enunciado 2 Posición, velocidad y aceleración 2.1 Determinación de la posición 2.2 Velocidad 2.3 Aceleración

1 Enunciado

Una pequeña anilla se halla ensartada en las dos barras rotatorias de la figura. Las dos barras giran alrededor de puntos fijos O y A que distan una cantidad b. Las dos barras giran en sentido positivo, la de O con velocidad angular 2Ω y la de A con velocidad angular Ω. Inicialmente la barra de O se halla situada horizontalmente y la de A verticalmente.

1. Determine la posición, velocidad y aceleración de la anilla como función del tiempo.
2. Para el instante en que tg(Ωt) = 1 / 2 halle
   1. La posición, velocidad y aceleración de la anilla.
   2. El triedro de Frenet referido a la base canónica
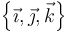
   3. Las componentes intrínsecas de la aceleración (escalares).
   4. El radio y el centro de curvatura.

2 Posición, velocidad y aceleración

2.1 Determinación de la posición

2.2 Velocidad

2.3 Aceleración