Dinámica impulsiva analítica (CMR)

De Laplace

(Diferencias entre revisiones)

Revisión de 00:07 4 feb 2017

Contenido

1 Introducción
2 Impulsos generalizados
3 Ecuaciones de Lagrange impulsivas
4 Fuerzas de reacción impulsivas

1 Introducción

Al estudiar la mecánica en su formulación vectorial introducimos las fuerzas impulsivas como aquellas que era de una gran intensidad pero actuaban durante un breve periodo de tiempo. Idealmente, una fuerza impulsiva sería una de intensidad infinita que actúa durante un intervalo infinitesimal. Cuando actúa una fuerza de este tipo, se dice que el sistema ha experimentado una percusión.

Para caracterizar una fuerza impulsiva que actúa entre $t 1$ y $t 1 + Δ t$ , definimos el impulso

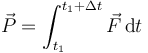
$\vec{P}=\int_{t_1}^{t_1+\Delta t}\vec{F}\,\mathrm{d}t$

Esta cantidad mide la magnitud de la fuerza impulsiva, pero no es una fuerza, ya que se mide en N·s.

El efecto de una percusión sobre una partícula es modificar su velocidad, pero no su posición

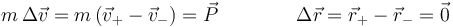
$m\,\Delta \vec{v}=m\left(\vec{v}_+-\vec{v}_-\right)=\vec{P}\qquad\qquad \Delta\vec{r}=\vec{r}_+-\vec{r}_-=\vec{0}$

Aquí el incremento se calcula como la diferencia entre el estado justo tras la percusión menos el estado inmediatamente previo a ella.

La posición no cambia porque se trata de la integral de la velocidad en el intervalo que dura la percusión. Dado que la velocidad no se hace infinita (aunque sea casi discontínua) y el intervalo tiende a 0, resulta que esta integral se anula.

Para el caso de un sistema de partículas con percusiones en los puntos $A i$ , tenemos los análogos al teorema de la cantidad de movimiento (TCM)

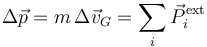
$\Delta \vec{p}=m\,\Delta \vec{v}_G=\sum_i \vec{P}_i^\mathrm{ext}$

y del teorema del momento cinético

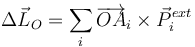
$\Delta \vec{L}_O=\sum_i \overrightarrow{OA}_i\times\vec{P}^{ext}_i$

Aquí O es cualquier punto, no necesariamente inmóvil o el CM, aunque suele aplicarse a estos dos últimos casos.

Las percusiones internas se anulan como consecuencia de la tercera ley de Newton.

Las percusiones, tanto internas como externas, pueden ser aplicadas o pueden ser de reacción vincular.

2 Impulsos generalizados

Al escribir las ecuaciones de la mecánica en términos de coordenadas generalizadas, aparecen las fuerzas generalizadas

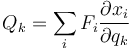
$Q_k = \sum_i F_i \frac{\partial x_i}{\partial q_k}$

La generalización a fuerzas impulsivas es inmediata. Si consideramos que $F i$ es una fuerza impulsiva e integramos sobre la duración de la percusión resulta

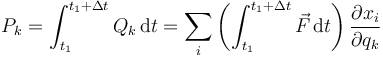
$P_k = \int_{t_1}^{t_1+\Delta t}Q_k\,\mathrm{d}t=\sum_i \left(\int_{t_1}^{t_1+\Delta t}\vec{F}\,\mathrm{d}t\right) \frac{\partial x_i}{\partial q_k}$

A esta cantidad se la conoce como impulso generalizado. Puede corresponder a un impulso en una dirección o ser un par impulsivo que produce un giro.

3 Ecuaciones de Lagrange impulsivas

Una vez definidos los impulsos generalizados, las ecuaciones de la dinámica analítica en presencia de fuerzas impulsivas pueden escribirse de diferentes formas. Aquí solo consideraremos el caso más simple.

Las ecuacionesde Lagrange para un sistema pueden escribirse en la forma

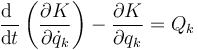
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial\dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q_k$

Aquí $Q k$ incluye, en principio, todas las fuerzas: conservativas, no conservativas y de reacción vincular. En cada categoría, algunas pueden ser no impulsivas (actúan de forma distribuida en el tiempo, como el peso) o ser impulsiva (por ejemplo, colisiones). Separando en estas dos categorías

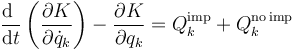
$\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial\dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q^\mathrm{imp}_k+Q^\mathrm{no\,imp}_k$

Si ahora integramos esta ecuación respecto al tiempo sobre el breve intervalo que dura la percusión, obtenemos los siguientes cuatro términos:

Para las fuerzas impulsivas

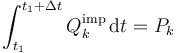
$\int_{t_1}^{t_1+\Delta t}Q^\mathrm{imp}_k\,\mathrm{d}t=P_k$

Para las no impulsivas

$\int_{t_1}^{t_1+\Delta t}Q^\mathrm{no\,imp}_k\,\mathrm{d}t=0$

La razón de que se anule esta integral es que estamos considerando un integrando finito (ya que las fuerzas no impulsivas, como el peso, no son infinitamente intensas, sino mucho más débiles que las impulsivas) sobre un intervalo infinitesimal.

De los términos del primer miembro, tenemos la para la derivada temporal de los momentos generalizados

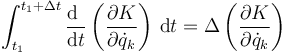
$\int_{t_1}^{t_1+\Delta t}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial\dot{q}_k}\right)\,\mathrm{d}t=\Delta\left(\frac{\partial K}{\partial\dot{q}_k}\right)$

ya que la integral de una derivada da el incremento de la función original.

Por último tenemos que

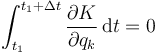
$\int_{t_1}^{t_1+\Delta t}\frac{\partial K}{\partial q_k}\,\mathrm{d}t=0$

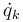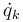Este término se anula por la misma razón que el de las fuerzas no impulsivas. La energía cinética es una función de las coordenadas $q k$ y velocidades $\dot{q}_k$ (no de las aceleraciones). Su derivada respecto a una coordenada es otra función de las $q k$ y $\dot{q}_k$ . Ninguna de estas cantidades es infinita, aunque pueda ser discontinua. Por tanto su integral sobre un intervalo infinitesimal se anula.

Reuniendo todo esto queda finalmente

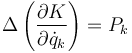
$\Delta\left(\frac{\partial K}{\partial\dot{q}_k}\right)=P_k$

es decir, lo que varía el momento generalizado es igual al impulso generalizado.

4 Fuerzas de reacción impulsivas

@@ Línea 49: / Línea 49: @@
 Aquí <math>Q_k</math> incluye, en principio, todas las fuerzas: conservativas, no conservativas y de reacción vincular. En cada categoría, algunas pueden ser no impulsivas (actúan de forma distribuida en el tiempo, como el peso) o ser impulsiva (por ejemplo, colisiones). Separando en estas dos categorías
-<center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial\dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q^\mathrm{imp}_k+Q^\mathrm{no\ imp}_k</math></center>
+<center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial\dot{q}_k}\right)-\frac{\partial K}{\partial q_k}=Q^\mathrm{imp}_k+Q^\mathrm{no\,imp}_k</math></center>
+Si ahora integramos esta ecuación respecto al tiempo sobre el breve  intervalo que dura la percusión, obtenemos los siguientes cuatro términos:
+Para las fuerzas impulsivas
+<center><math>\int_{t_1}^{t_1+\Delta t}Q^\mathrm{imp}_k\,\mathrm{d}t=P_k</math></center>
+Para las no impulsivas
+<center><math>\int_{t_1}^{t_1+\Delta t}Q^\mathrm{no\,imp}_k\,\mathrm{d}t=0</math></center>
+La razón de que se anule esta integral es que estamos considerando un integrando finito (ya que las fuerzas no impulsivas, como el peso, no son infinitamente intensas, sino mucho más débiles que las impulsivas) sobre un intervalo infinitesimal.
+De los términos del primer miembro, tenemos la para la derivada temporal de los momentos generalizados
+<center><math>\int_{t_1}^{t_1+\Delta t}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial K}{\partial\dot{q}_k}\right)\,\mathrm{d}t=\Delta\left(\frac{\partial K}{\partial\dot{q}_k}\right)</math></center>
+ya que la integral de una derivada da el incremento de la función original.
+Por último tenemos que
+<center><math>\int_{t_1}^{t_1+\Delta t}\frac{\partial K}{\partial q_k}\,\mathrm{d}t=0</math></center>
+Este término se anula por la misma razón que el de las fuerzas no impulsivas. La energía cinética es una función de las coordenadas <math>q_k</math> y velocidades <math>\dot{q}_k</math> (no de las aceleraciones). Su derivada respecto a una coordenada es otra función de las <math>q_k</math> y <math>\dot{q}_k</math>. Ninguna de estas cantidades es infinita, aunque pueda ser discontinua. Por tanto su integral sobre un intervalo infinitesimal se anula.
+Reuniendo todo esto queda finalmente
+<center><math>\Delta\left(\frac{\partial K}{\partial\dot{q}_k}\right)=P_k</math></center>
+es decir, lo que varía el momento generalizado es igual al impulso generalizado.
 ==Fuerzas de reacción impulsivas==
 [[Categoría:Mecánica analítica (CMR)]]

Dinámica impulsiva analítica (CMR)

De Laplace

Revisión de 00:07 4 feb 2017

Contenido

1 Introducción

2 Impulsos generalizados

3 Ecuaciones de Lagrange impulsivas

4 Fuerzas de reacción impulsivas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES