Dinámica impulsiva analítica (CMR)
De Laplace
Contenido |
1 Introducción
Al estudiar la mecánica en su formulación vectorial introducimos las fuerzas impulsivas como aquellas que era de una gran intensidad pero actuaban durante un breve periodo de tiempo. Idealmente, una fuerza impulsiva sería una de intensidad infinita que actúa durante un intervalo infinitesimal. Cuando actúa una fuerza de este tipo, se dice que el sistema ha experimentado una percusión.
Para caracterizar una fuerza impulsiva que actúa entre t1 y t1 + Δt, definimos el impulso
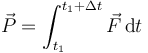
Esta cantidad mide la magnitud de la fuerza impulsiva, pero no es una fuerza, ya que se mide en N·s.
El efecto de una percusión sobre una partícula es modificar su velocidad, pero no su posición
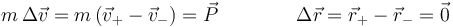
Aquí el incremento se calcula como la diferencia entre el estado justo tras la percusión menos el estado inmediatamente previo a ella.
La posición no cambia porque se trata de la integral de la velocidad en el intervalo que dura la percusión. Dado que la velocidad no se hace infinita (aunque sea casi discontínua) y el intervalo tiende a 0, resulta que esta integral se anula.
Para el caso de un sistema de partículas con percusiones en los puntos Ai, tenemos los análogos al teorema de la cantidad de movimiento (TCM)
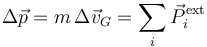
y del teorema del momento cinético
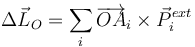
Aquí O es cualquier punto, no necesariamente inmóvil o el CM, aunque suele aplicarse a estos dos últimos casos.
Las percusiones internas se anulan como consecuencia de la tercera ley de Newton.
Las percusiones, tanto internas como externas, pueden ser aplicadas o pueden ser de reacción vincular.
2 Impulsos generalizados
Al escribir las ecuaciones de la mecánica en términos de coordenadas generalizadas, aparecen las fuerzas generalizadas
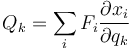
La generalización a fuerzas impulsivas es inmediata. Si consideramos que Fi es una fuerza impulsiva e integramos sobre la duración de la percusión resulta
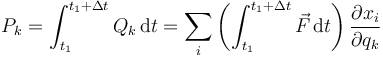
A esta cantidad se la conoce como impulso generalizado. Puede corresponder a un impulso en una dirección o ser un par impulsivo que produce un giro.
3 Ecuaciones de Lagrange impulsivas
Una vez definidos los impulsos generalizados, las ecuaciones de la dinámica analítica en presencia de fuerzas impulsivas pueden escribirse de diferentes formas. Aquí solo consideraremos el caso más simple.
Las ecuacionesde Lagrange para un sistema pueden escribirse en la forma
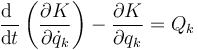
Aquí Qk incluye, en principio, todas las fuerzas: conservativas, no conservativas y de reacción vincular. En cada categoría, algunas pueden ser no impulsivas (actúan de forma distribuida en el tiempo, como el peso) o ser impulsiva (por ejemplo, colisiones). Separando en estas dos categorías
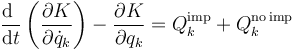
Si ahora integramos esta ecuación respecto al tiempo sobre el breve intervalo que dura la percusión, obtenemos los siguientes cuatro términos:
Para las fuerzas impulsivas
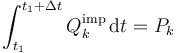
Para las no impulsivas

La razón de que se anule esta integral es que estamos considerando un integrando finito (ya que las fuerzas no impulsivas, como el peso, no son infinitamente intensas, sino mucho más débiles que las impulsivas) sobre un intervalo infinitesimal.
De los términos del primer miembro, tenemos la para la derivada temporal de los momentos generalizados
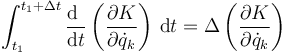
ya que la integral de una derivada da el incremento de la función original.
Por último tenemos que
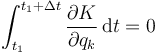
Este término se anula por la misma razón que el de las fuerzas no impulsivas. La energía cinética es una función de las coordenadas qk y velocidades 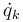 (no de las aceleraciones). Su derivada respecto a una coordenada es otra función de las qk y
(no de las aceleraciones). Su derivada respecto a una coordenada es otra función de las qk y 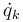 . Ninguna de estas cantidades es infinita, aunque pueda ser discontinua. Por tanto su integral sobre un intervalo infinitesimal se anula.
. Ninguna de estas cantidades es infinita, aunque pueda ser discontinua. Por tanto su integral sobre un intervalo infinitesimal se anula.
Reuniendo todo esto queda finalmente
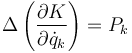
es decir, lo que varía el momento generalizado es igual al impulso generalizado.
4 Fuerzas de reacción impulsivas
La presencia de vínculos provoca la aparición de fuerzas impulsivas de reacción. Éstas pueden deberse a varias causas, según el tipo de vínculo. Pueden clasificarse cuatro casos según los vínculos existan antes, durante y después de la percusión:
- Vínculos preexistentes persistentes
- son aquellos que existen antes, durante y después de la percusión.
- Llevan aparejados fuerzas impulsivas en respuesta a otras percusiones. Así, por ejemplo, una viga empotrada que es golpeada en algún punto provoca la aparición d euna fuerza impulsiva y de un par impulsivo en el mpunto de empotramiento.
- Vínculos impuestos persistentes
- son los que existen durante y después de la percusión, pero no antes de ella. Es lo que ocurre, por ejemplo al tensarse el hilo de un péndulo flexible.
- Esta situación implica fuerzas impulsivas porque las velocidades previas a la imposición pueden no cumplir el vínculo y por tanto deben cambiar bruscamente. Esto se manifiesta en que el hilo pega un tirón al tensarse.
- Vínculos anulados
- son los que existen antes y durante la percusión, pero no después de ella. Siguiendo con el ejemplo del péndulo, sería el caso de que se rompa la cuerda.
- A diferencia de la imposición, la anulación no tiene por qué provocar fuerzas impulsivas. La razón es que la eliminación del vinculo significa una mayor generalidad en las velocidades posibles y por tanto las velocidades previas ya cumplen las restricciones posteriores, que son menores.
- Vinculos impulsivos
- son los que solo existen durante el tiempo que dura la percusión. Así, por ejemplo, en una colisión entre dos sólidos, durante el tiempo que dura ésta, se cumple la condición de impenetrabilidad y por tanto la velocidad normal relativa debe ser nula.
- Dado que en los análisis de percusiones lo que se estudia es la relación entre el estado previo y el posterior, y no lo que ocurre durante, los vínculos impulsivos requieren algún tipo de modelo de cómo es esa colisión, ya que no es lo mismo que los sólidos se comporten como cuerpos rígidos a que sean deformables. Es por ello, que se habla de colisiones elásticas o inelásticas, como forma empírica de caracterizar la colisión sin entrar en el detalle de cómo se produce.

Cuando tenemos un vínculo escrito en la forma
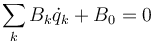
admitimos que los coeficientes Bk no dependen de las velocidades, sino solo de las coordenadas. Sabemos que en este caso, las componentes de las fuerzas de reacción son de la forma
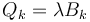
siendo λ el multiplicador de Lagrange correspondiente.
Si integramos esta ecuación respecto al tiempo, obtenemos los impulsos generalizados
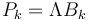
donde los coeficientes son los mismos ya que si solo dependen de las coordenadas y estas no cambian durante la percusión, los coeficientes son constantes para esta integral. Por tanto solo habría que integrar el multiplicador de Lagrange lo que nos da una cierta cantidad, también desconocida, que habrá que hallar en la solución del problema.
Esto es una aproximación, ya que supone que la ecuación del vínculo no se ve afectada por la percusión, lo cual es discutible. En la colisión de dos esferas de acero, por ejemplo, las fuerzas pueden ser tan importantes como para producir una deformación apreciable, incumpliéndose la condición de rigidez.
Admitiendo que las fuerzas impulsivas de reacción cumplen esta condición, la ecuación de Lagrange para la dinámica impulsiva con diversos vínculos queda en la forma
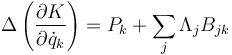
donde aquí las Pk ya solo incluyen las fuerzas impulsivas aplicadas.
La estrategia más efectiva para abordar la imposición de vínculos suele ser el elegir las coordenadas de manera que el nuevo vínculo se convierta en trivial de manera que el impulso generalizado aparezca en una sola de las ecuaciones de Lagrange.
Supongamos una masa que cuelga de un hilo flexible de longitud 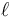 . Inicialmente la masa se halla a la misma altura que el punto al que se encuentra atado el hilo, y a una distancia d de este punto. Se deja caer la masa. ¿Cuánto vale la tensión impulsiva en el hilo?
. Inicialmente la masa se halla a la misma altura que el punto al que se encuentra atado el hilo, y a una distancia d de este punto. Se deja caer la masa. ¿Cuánto vale la tensión impulsiva en el hilo?
Si empleamos coordenadas polares, la ecuación del vínculo es
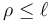
Antes de que se tense se cumple la desigualdad y es como si este vínculo no existiera. Una vez tensado se cumple la igualdad.
La energía cinética de la partícula es
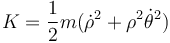
Cuando el hilo se tensa se impone el vínculo

lo que nos da las ecuaciones para el impulso

Obsérvese que el peso no aparece en estas ecuaciones, por ser una fuerza no impulsiva, su efecto es despreciable en este breve intervalo de tiempo.
Calculando los momentos conjugados nos queda

La segunda de las ecuaciones nos permite calcular la velocidad justo después del tirón, que es la misma que antes de él. La velocidad anterior se halla resolviendo las ecuaciones de movimiento previas. En este caso es simple por conservación de la energía y proyectando posteriormente en las direcciones radial y acimutal

Aquí h es lo que desciende y θ0 el ángulo que forma con la vertical en el momento en que se tensa

Por tanto, tras el tirón
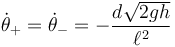
La magnitud de la percusión la obtenemos del salto en la velocidad radial
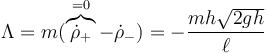
Es negativo porque va en la dirección radial hacia adentro. Si el tirón se produce en un tiempo Δt la tensión impulsiva tendrá el valor
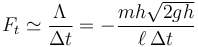
Esta cantidad puede ser muy elevada, por lo que podría llegar a romperse el hilo (o escaparse de las manos).






