Leyes de conservación en mecánica analítica (CMR)
De Laplace
| Línea 45: | Línea 45: | ||
* En el caso de que <math>q_1</math> represente una coordenada cartesiana, su momento conjugado representa la cantidad de movimiento en dicha dirección. Por tanto, si el sistema tiene ''simetría traslacional'', es decir, no cambia al realizar un desplzamiento rectilíneo, entonces se conserva una componente de la cantidad de movimiento. | * En el caso de que <math>q_1</math> represente una coordenada cartesiana, su momento conjugado representa la cantidad de movimiento en dicha dirección. Por tanto, si el sistema tiene ''simetría traslacional'', es decir, no cambia al realizar un desplzamiento rectilíneo, entonces se conserva una componente de la cantidad de movimiento. | ||
| - | {{ejemplo|'''Péndulo colgado de un | + | {{ejemplo|'''Péndulo colgado de un carrito''' |
| + | |||
| + | [[Archivo:pendulo-carrito.png|right]] | ||
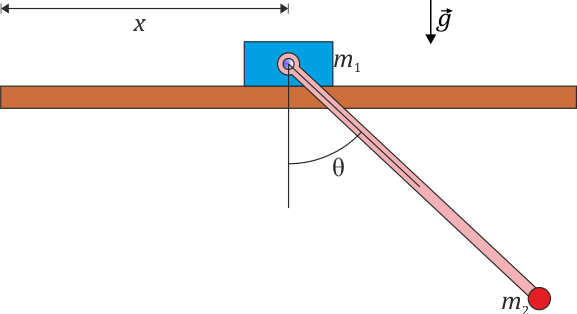
Supongamos un péndulo simple de masa <math>m_2</math> que cuelga de una varilla ideal, rígida y sin masa, de longitud <math>\ell</math>, cuyo otro extremo no está articulado a un punto fijo sino a un carrito de masa <math>m_1</math> que puede deslizar sin rozamiento por un eje horizontal. El péndulo solo puede oscilar en el plano vertical. En ese caso el sistema tiene 2 grados de libertad y podemos poner las dos posiciones como | Supongamos un péndulo simple de masa <math>m_2</math> que cuelga de una varilla ideal, rígida y sin masa, de longitud <math>\ell</math>, cuyo otro extremo no está articulado a un punto fijo sino a un carrito de masa <math>m_1</math> que puede deslizar sin rozamiento por un eje horizontal. El péndulo solo puede oscilar en el plano vertical. En ese caso el sistema tiene 2 grados de libertad y podemos poner las dos posiciones como | ||
| Línea 72: | Línea 74: | ||
* En el caso de que <math>q_1</math> represente una coordenada angular en torno a un eje, su momento conjugado representa el momento cinético asociado a giros en torno al eje. Por tanto, si el sistema tiene ''simetría de revolución'', es decir, no cambia al realizar un desplzamiento en torno al eje, entonces se conserva una componente del momento cinético. | * En el caso de que <math>q_1</math> represente una coordenada angular en torno a un eje, su momento conjugado representa el momento cinético asociado a giros en torno al eje. Por tanto, si el sistema tiene ''simetría de revolución'', es decir, no cambia al realizar un desplzamiento en torno al eje, entonces se conserva una componente del momento cinético. | ||
| + | {{ejemplo|'''Fuerzas centrales''' | ||
| + | |||
| + | Supongamos una partícula sometida a una fuerza central dependiente sólo de la distancia al origen de coordenadas. Si esta partícula se mueve en el plano OXY su lagrangiana en coordenadas polares será de la forma | ||
| + | |||
| + | <center><math>\mathcal{L}=\frac{1}{2}m\left(\dot{\rho}^2+\rho^2\dot{\theta}^2\right)-U(\rho)</math></center> | ||
| + | |||
| + | En esta lagrangiana el ángulo <math>\theta</math> es cíclico, por lo que su momento conjugado es una constante de movimiento | ||
| + | |||
| + | <center><math>p_\theta=\frac{\partial\mathcal{L}}{\partial\dot{\theta}=m\rho^2\dot{\theta}</math></center> | ||
| + | |||
| + | Este momento representa la componente Z del mómento cinético respecto al origen de coordenadas. | ||
| + | }} | ||
==Función de Routh== | ==Función de Routh== | ||
Cuando se tiene una coordenada cíclica <math>q_1</math> se sabe que su momento conjugado <math>p_1</math> es una constante de valor <math>\beta_1</math>. A partir de esta constante puede normalmente despejarse la velocidad generalizada <math>\dot{q}_1</math>. Puede plantearse entonces la reducción del sistema en una variable aprovechando que <math>q_1</math> no aparece en la lagrangiana y que <math>\dot{q}_1</math> puede ponerse en función del resto de coordenadas y constantes. | Cuando se tiene una coordenada cíclica <math>q_1</math> se sabe que su momento conjugado <math>p_1</math> es una constante de valor <math>\beta_1</math>. A partir de esta constante puede normalmente despejarse la velocidad generalizada <math>\dot{q}_1</math>. Puede plantearse entonces la reducción del sistema en una variable aprovechando que <math>q_1</math> no aparece en la lagrangiana y que <math>\dot{q}_1</math> puede ponerse en función del resto de coordenadas y constantes. | ||
Revisión de 18:50 17 ene 2017
Contenido |
1 Introducción
Una constante de movimiento o integral primera es una función dependiente de las coordenadas, velocidades y posiblemente el tiempo, cuyo valor es el mismo en todo instante.
Si el sistema viene descrito por una serie de coordenadas generalizadas qk, una constante de movimiento cumpliría
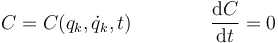
Desarrollando aquí la derivada total queda la condición para que C sea una constante
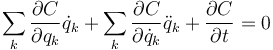
A partir de las ecuaciones de Lagrange pueden obtenerse expresiones para las segundas derivadas que, sustituidas aquí deberían llevar a la anulación del primer término, si efectivamente C es una constante.
La búsqueda de constantes de movimiento es una tarea que puede ser complicada, ya que las posibles combinaciones de coordenadas generalizadas son infinitas. Aquí conideraremos solo los casos matemáticamente más simples.
2 Coordenadas cíclicas
Suponemos el caso más simple de coordenadas generalizadas independientes y ausencia de fuerzas no conservativas. En estas condiciones se satisfacen las ecuaciones de Lagrange
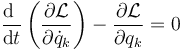
siendo la lagrangiana del sistema
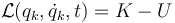
Una coordenada q1 se dice cclica o ignorable si no aparece en la lagrangiana, es decir
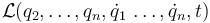
y por tanto se anula derivada parcial
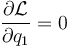
Esto implica, de acuerdo con las ecuaciones de Lagrange, que
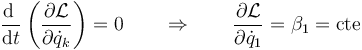
A la derivada parcial
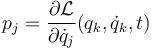
se la denomina el momento conjugado de la coordenada qj. Por tanto, si q1 es cíclica su momento conjugado p1 es una constante de movimiento de valor β1 dado por las condiciones iniciales.
Hay una estrecha relación entre las constantes de movimiento y las simetrías del sistema.
- En el caso de que q1 represente una coordenada cartesiana, su momento conjugado representa la cantidad de movimiento en dicha dirección. Por tanto, si el sistema tiene simetría traslacional, es decir, no cambia al realizar un desplzamiento rectilíneo, entonces se conserva una componente de la cantidad de movimiento.
Supongamos un péndulo simple de masa m2 que cuelga de una varilla ideal, rígida y sin masa, de longitud 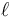 , cuyo otro extremo no está articulado a un punto fijo sino a un carrito de masa m1 que puede deslizar sin rozamiento por un eje horizontal. El péndulo solo puede oscilar en el plano vertical. En ese caso el sistema tiene 2 grados de libertad y podemos poner las dos posiciones como
, cuyo otro extremo no está articulado a un punto fijo sino a un carrito de masa m1 que puede deslizar sin rozamiento por un eje horizontal. El péndulo solo puede oscilar en el plano vertical. En ese caso el sistema tiene 2 grados de libertad y podemos poner las dos posiciones como
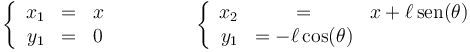
siendo la energía cinética
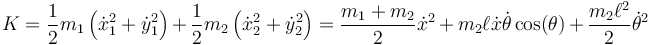
y la potencial
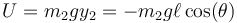
restando llegamos a la lagrangiana
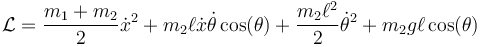
En esta lagrangiana, x es cíclica. Esto expresa que es independiente el punto del eje horizontal donde coloquemos el carrito, siempre que se mantenga la posición relativa entre éste y el péndulo. Hallamos el momento conjugado
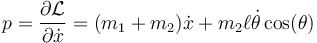
Esta cantidad es una constante de movimiento del problema. Físicamente representa la componente horizontal de la cantidad de movimiento. Cuando la lenteja del péndulo se mueve hacia la derecha, el carrito se ve impulsado hacia la izquierda y viceversa.
- En el caso de que q1 represente una coordenada angular en torno a un eje, su momento conjugado representa el momento cinético asociado a giros en torno al eje. Por tanto, si el sistema tiene simetría de revolución, es decir, no cambia al realizar un desplzamiento en torno al eje, entonces se conserva una componente del momento cinético.
Supongamos una partícula sometida a una fuerza central dependiente sólo de la distancia al origen de coordenadas. Si esta partícula se mueve en el plano OXY su lagrangiana en coordenadas polares será de la forma
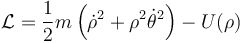
En esta lagrangiana el ángulo θ es cíclico, por lo que su momento conjugado es una constante de movimiento
Este momento representa la componente Z del mómento cinético respecto al origen de coordenadas.
3 Función de Routh
Cuando se tiene una coordenada cíclica q1 se sabe que su momento conjugado p1 es una constante de valor β1. A partir de esta constante puede normalmente despejarse la velocidad generalizada 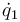 . Puede plantearse entonces la reducción del sistema en una variable aprovechando que q1 no aparece en la lagrangiana y que
. Puede plantearse entonces la reducción del sistema en una variable aprovechando que q1 no aparece en la lagrangiana y que 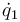 puede ponerse en función del resto de coordenadas y constantes.
puede ponerse en función del resto de coordenadas y constantes.
No obstante, el procedimiento a seguir no consiste en la simple sustitución en 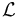 . Esto produciría ecuaciones incorrectas. Para la reducción del sistema deben seguirse los siguientes pasos:
. Esto produciría ecuaciones incorrectas. Para la reducción del sistema deben seguirse los siguientes pasos:
- Identifíquese la coordenada cíclica q1 (puede haber más de una) que no aparece en la lagrangiana (¡ojo! sí que aparece
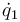 )
)
- Calcúlese su momento conjugado
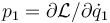 . Este momento es una función de
. Este momento es una función de 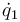 y del resto de coordenadas y velocidades, siendo una constante de movimiento.
y del resto de coordenadas y velocidades, siendo una constante de movimiento.
- Hállese, si esposible, el valor concreto, β1 del momento generalizado a partir de las condiciones iniciales.
- Despéjese la velocidad generalizada
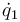 de la expresión de p1
de la expresión de p1
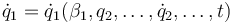
- Sustitúyase en la lagrangiana
- Calcúlese la denominada función de Routh, que equivale a la lagrangiana reducida
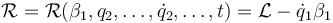
- Las nuevas ecuaciones de movimiento, ya con un grado de libertad menos, se calculan con esta función
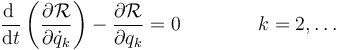
- Si fuera necesario hallar q1 se calcula integrando respecto al tiempo la ecuación
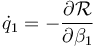
Si hay más de una coordenada cíclica, la correspondiente función de Routh se halla como
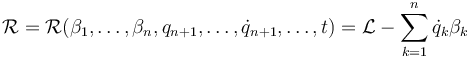
4 Energía y función hamiltoniana
4.1 Función hamiltoniana
El tiempo t que aparece en la lagrangiana no es una coordenada generalizada, ya que su papel en las ecuaciones es diferente al resto. No obstante, de la misma manera que la ausencia de q1 implica una ley de conservación de su momento conjugado, la independencia temporal de la lagrangiana también implica una constante de movimiento.
En un sistema en el que todas las coordenadas son independientes y no hay presentes fuerzas no conservativas, cuando la lagrangiana es independiente del tiempo
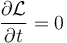
la constante de movimiento no es la propia lagrangiana (es decir,de que se anule la derivada parcial no se deduce que se anule la derivada total), sino que la cantidad que se conserva es la denominada función hamiltoniana
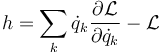
Esta función coincide en muchos casos, pero no siempre, con la energía mecánica del sistema. Por ello, se dice que esta cantidad conservada es del tipo energía.
4.2 Demostración
4.3 Estructura de la lagrangiana
Podemos descomponer la lagrangiana en suma de varios términos, de manera que obtengamos una respuesta clara de cuál es el aspecto de la función h, cuya expresión anterior no hace evidente que se trata de algo relacionado con la energía.
Cuando se definen las coordenadas generalizadas a través de las relaciones

se llega a una relación entre velocidades
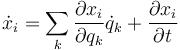
Si sustituimos esta expresión en la energía cinética
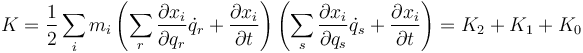
donde los tres sumandos vienen dados por
- Término cuadrático
- es una combinación de productos de las velocidades generalizadas

- Término lineal
- es combinación de las velocidades generalizadas
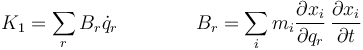
- Término independiente
- no depende de las velocidades generalizadas
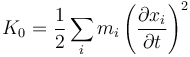
En el caso de que en la definición de las coordenadas generalizadas no aparezca el tiempo los términos K1 y K0 se anulan y solo aparece K2
Cuando se hace esta descomposición puede demostrarse desarrollando y sustituyendo, que la función hamiltoniana es igual a
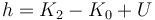
por lo cual:
- Si K0 = 0 se anula la función hamiltoniana coincide con la energía mecánica del sistema.
- Si
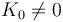 la función hamiltoniana no coincide con la energía mecánica, pero se parece a ella.
la función hamiltoniana no coincide con la energía mecánica, pero se parece a ella.
Un caso típico en el que la hamiltoniana no coincide con la energía mecánica es aquél en que se emplea un sistema de referencia en rotación.
Supongamos una partícula que se mueve en el plano OXY, estando su posición descrita por las coordenadas cartesianas (x,y) o por polares (ρ,θ). Si esa misma partícula la analizamos desde un sistema de referencia que gira con velocidad angular constante Ω, en este sistema sus coordenadas polares serán 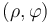 con
con
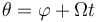
de manera que la energía cinética de esta partícula vale
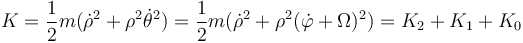
con
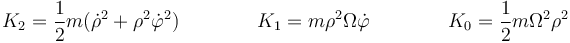
Si esta partícula se mueve sometida a una fuerza conservativa, la cantidad conservada es
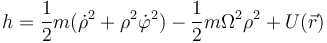
es decir,tiene la misma forma que el de una partícula en ausencia de rotación del sistema de referencia, pero con una energía potencial diferente
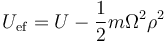
A este término extra, que es como el de un oscilador armónico pero cambiado de signo, se lo denomina potencial centrífugo y permite describir los sistemas como si la fuerza centrífuga estuviera presente y tendiera al mínimo potencial centrífugo.