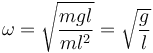Energía y leyes de conservación (CMR)
De Laplace
(Página creada con '==Integrales primeras== Una '''constante de movimiento''' (también llamada '''integral primera''') es una magnitud función de la posición, velocidad de la partícula (o de la…') |
|||
| Línea 22: | Línea 22: | ||
Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. A continuación estudiaremos tres magnitudes, construidas a partir de la posición y la velocidad, cuyas leyes de evolución pueden determinarse a partir de las leyes de Newton. Estas cantidades, si se dan las condiciones adecuadas, son candidatas a ser constantes de movimiento, y por tanto son las primeras candidatas cuando en un problema se buscan integrales primeras. Estas magnitudes son: | Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. A continuación estudiaremos tres magnitudes, construidas a partir de la posición y la velocidad, cuyas leyes de evolución pueden determinarse a partir de las leyes de Newton. Estas cantidades, si se dan las condiciones adecuadas, son candidatas a ser constantes de movimiento, y por tanto son las primeras candidatas cuando en un problema se buscan integrales primeras. Estas magnitudes son: | ||
| - | * [[ | + | * La cantidad de movimiento |
| - | + | * El momento cinético o momento angular | |
| - | * [[Trabajo y energía ( | + | * La energía mecánica |
| + | |||
| + | ==Cantidad de movimiento== | ||
| + | ===Definición=== | ||
| + | Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad | ||
| + | |||
| + | <center><math>\vec{p}=m\vec{v}\,</math></center> | ||
| + | |||
| + | Sus dimensiones son <math>MLT^{-1}</math> y sus unidades en el SI son <math>\mathrm{N}\cdot\mathrm{s}</math> (o <math>\mathrm{kg}\cdot\mathrm{m}/\mathrm{s}</math>) | ||
| + | |||
| + | ===Teorema de la cantidad de movimiento=== | ||
| + | A partir de la definición es inmediato que | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}=m\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\vec{a} = \vec{F}</math></center> | ||
| + | |||
| + | esto es, la derivada respecto al tiempo de la cantidad de movimiento es igual a la resultante de las fuerzas aplicadas sobre la partícula. | ||
| + | ===Impulso=== | ||
| + | En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante <math>\vec{p}_1</math>. Entonces es sometida a una fuerza <math>\vec{F}(t)</math> durante un intervalo entre <math>t_1</math> y <math>t_2</math> (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante <math>\vec{p}_2</math>. Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. Integrando en la segunda ley de Newton obtenemos | ||
| + | |||
| + | <center><math>\Delta \vec{p}=\vec{p}_2-\vec{p}_1 = \int_{t_1}^{t_2}\vec{F}(t)\,\mathrm{d}t</math></center> | ||
| + | |||
| + | [[Imagen:raquetbol.gif|right]] | ||
| + | |||
| + | Esta integral de la fuerza sobre un intervalo recibe el nombre de '''impulso''', por lo que la igualdad anterior establece que | ||
| + | |||
| + | :“''El incremento de la cantidad de movimiento es igual al impulso recibido''” | ||
| + | |||
| + | Esta relación, aparentemente trivial, tiene su importancia en la teoría de [[Colisiones_de_dos_part%C3%ADculas|colisiones]] y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso. | ||
| + | |||
| + | Así, por ejemplo, en un saque de tenis, la rapidez de la pelota pasa de ser prácticamente nula a valer unos 60 m/s. Dado que la masa de una pelota es de 68 g, esto supone un impulso | ||
| + | |||
| + | <center><math>\Delta p = m v - 0 = 4.08\,\mathrm{N}\cdot\mathrm{s}</math></center> | ||
| + | |||
| + | No conocemos la fuerza instantánea sobre la pelota, puesto que su deformación la convierte en un problema muy complejo. Podemos hallar la fuerza media, si conocemos el tiempo de colisión. Un valor típico podrían ser 30 ms, lo que nos da una fuerza media | ||
| + | |||
| + | <center><math>F_m = \frac{\Delta p}{\Delta t} = \frac{4.08\,\mathrm{N}\cdot\mathrm{s}}{0.03\,\mathrm{s}}=136\,\mathrm{N}</math></center> | ||
| + | |||
| + | Por comparación, esta fuerza es 2000 veces el peso, o lo que es lo mismo, la pelota experimenta una aceleración de unos 200''g''. | ||
| + | |||
| + | ===Colisión con una pared=== | ||
| + | Un ejemplo de impulso lo tenemos en una colisión elástica con una pared. En este caso, la fuerza actúa sobre un tiempo muy corto <math>\epsilon</math>, pero es capaz de producir un impulso | ||
| + | |||
| + | <center><math>\Delta \vec{p}=\int_{t_0}^{t_0+\epsilon}\vec{F}\,\mathrm{d}t</math></center> | ||
| + | |||
| + | Carecemos de una expresión para la fuerza (aunque se puede modelar como una fuerza elástica). Podemos determinar el impulso a partir de su efecto. | ||
| + | |||
| + | ====Pared estacionaria==== | ||
| + | Si tenemos una partícula de masa <math>m</math> que impacta frontalmente con una superficie inmóvil se produce un cambio en la velocidad de la partícula, de forma que | ||
| + | |||
| + | * La componente tangente a la superficie no cambia | ||
| + | * La componente normal cambia de signo. | ||
| + | |||
| + | Supongamos que la superficie es el plano <math>z=0</math>. En ese caso, si la velocidad inicial es | ||
| + | |||
| + | <center><math>\vec{v}_i = v_{x0}\vec{\imath}+v_{z0}\vec{k}</math></center> | ||
| + | |||
| + | la velocidad tras la colisión será | ||
| + | |||
| + | <center><math>\vec{v}_f = v_{x0}\vec{\imath}-v_{z0}\vec{k}</math></center> | ||
| + | |||
| + | siendo el impulso sobre la partícula | ||
| + | |||
| + | <center><math>\Delta\vec{p}=m\vec{v}_f-m\vec{v}_i=-2mv_{z0}\vec{k}</math></center> | ||
| + | |||
| + | Colisiones como esta explican el concepto de ''presión'' a nivel microscópico. Cada una de las partículas de un gas que choca contra las paredes de un recipiente transfiere una cierta cantidad de movimiento. El conjunto de todas las colisiones por unidad de tiempo es una fuerza media. La fuerza por unidad de superficie es la presión. | ||
| + | |||
| + | ====Pared en movimiento==== | ||
| + | Si la pared está en movimiento (caso de una raqueta que golpea una pelota), el cambio de signo se da en la velocidad relativa, no en la absoluta. | ||
| + | |||
| + | En el caso unidimensional, si la velocidad inicial de la partícula y de la pared valen | ||
| + | |||
| + | <center><math>\vec{v}_i = v_0\vec{\imath}\qquad \qquad \vec{V}=V\vec{\imath}</math></center> | ||
| + | |||
| + | la velocidad de la partícula relativa a la pared, antes de la colisión, es | ||
| + | |||
| + | <center><math>\vec{v}'_i=\vec{v}_i-\vec{V}=(v_0-V)\vec{\imath}</math></center> | ||
| + | |||
| + | Tras la colisión, esta velocidad relativa invierte su sentido | ||
| + | |||
| + | <center><math>\vec{v}'_f=-(v_0-V)\vec{\imath}</math></center> | ||
| + | |||
| + | por lo que la nueva velocidad absoluta es | ||
| + | |||
| + | <center><math>\vec{v}_f = \vec{v}'_f+\vec{V}=(2V-v_0)\vec{\imath}</math></center> | ||
| + | |||
| + | Vemos que tras la colisión, la partícula puede moverse más o menos rápido que antes, dependiendo de ambas velocidades. En particular, si la velocidad inicial es nula, sale disparada con una velocidad doble de la raqueta, y si la velocidad inicial es el doble de la de la raqueta, tras la colisión se queda clavada en el sitio. | ||
| + | |||
| + | El impulso en esta colisión es igual a | ||
| + | |||
| + | <center><math>\Delta \vec{p}=m\vec{v}_f-m\vec{v}_i=2m(V-v_0)\vec{\imath}</math></center> | ||
| + | |||
| + | ===Teorema de conservación=== | ||
| + | De la segunda ley de Newton es inmediato que: | ||
| + | |||
| + | :“''La cantidad de movimiento de una partícula permanece constante cuando la resultante de las fuerzas que actúan sobre ella es nula durante un intervalo de tiempo''” | ||
| + | |||
| + | <center><math>\vec{0}=\vec{F} = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}\qquad\Rightarrow\qquad \vec{p}=\vec{p}_0=\mathrm{cte}</math></center> | ||
| + | |||
| + | Puesto que la masa de la partícula permanece constante, si la cantidad de movimiento se conserva, la velocidad también permanece constante | ||
| + | |||
| + | <center><math>\vec{p}=\vec{p}_0=\mathrm{cte}</math>{{tose}}<math>\vec{v}=\frac{\vec{p}}{m}=\mathrm{cte}</math></center> | ||
| + | |||
| + | Por tanto, si la resultante de las fuerzas que actúan sobre la partícula se anula durante un intervalo de tiempo, la partícula se mueve uniformemente durante dicho periodo. | ||
| + | |||
| + | Esto no es exactamente lo mismo que lo que dice la Primera Ley de Newton, pues esta ley habla de partícula no sometida a ninguna interacción, mientras que el teorema de conservación se refiere a una partícula sometida a diferentes fuerzas, pero tales que su resultante es nula. | ||
| + | |||
| + | Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un [[cantidad de movimiento de un sistema de partículas|sistema de partículas]] es extremadamente útil. | ||
| + | |||
| + | ==Momento cinético== | ||
| + | ===Definiciones=== | ||
| + | |||
| + | [[Archivo:momento-cinetico.png|right]] | ||
| + | ====Momento cinético==== | ||
| + | Se define el ''momento cinético'' (o ''momento angular'') de una partícula respecto a un punto fijo O como | ||
| + | |||
| + | <center><math>\vec{L}_O = \vec{r}\times\vec{p}=m\vec{r}\times\vec{v}</math></center> | ||
| + | |||
| + | siendo | ||
| + | |||
| + | <center><math>\vec{r}=\overrightarrow{OP}</math></center> | ||
| + | |||
| + | el vector de posición del punto P relativa al punto O. | ||
| + | |||
| + | ====Momento de una fuerza==== | ||
| + | Se define el momento respecto a un punto fijo O de una fuerza aplicada en un punto P como el producto vectorial | ||
| + | |||
| + | <center><math>\vec{M}_O = \vec{r}\times\vec{F}=\overrightarrow{OP}\times\vec{F}</math></center> | ||
| + | |||
| + | Al momento de una fuerza también se lo denomina “el par de la fuerza” o (por contagio del inglés) el “torque”. | ||
| + | |||
| + | <center>[[Archivo:momento-fuerza.png]]</center> | ||
| + | |||
| + | El módulo del momento de una fuerza es igual a | ||
| + | |||
| + | <center><math>|\vec{M}_O| = |\vec{F}||\overrightarrow{OP}|\,\mathrm{sen}(\beta)</math></center> | ||
| + | |||
| + | pero | ||
| + | |||
| + | <center><math>d = |\overrightarrow{OP}|\,\mathrm{sen}(\beta)</math></center> | ||
| + | |||
| + | es la distancia a la llamada ''recta soporte'', que es aquella que pasa por P y tiene la dirección de la fuerza. Por tanto, el módulo del momento de la fuerza se puede escribir | ||
| + | |||
| + | <center><math>|\vec{M}_O| = |\vec{F}|d</math></center> | ||
| + | |||
| + | A la distancia <math>d</math> se la denomina “brazo del momento” o “brazo del par”. De aquí resulta que el valor del momento de una fuerza no depende de la posición exacta del punto P, sino solo de la recta soporte donde se halla. | ||
| + | |||
| + | La dirección del momento de la fuerza es perpendicular al plano definido por <math>\overrightarrow{OP}</math> y la fuerza (es decir, el que contiene a O y a la recta soporte). Su sentido lo da la regla de la mano derecha. Si O está a un lado de la recta soporte, el sentido del momento es hacia afuera del plano; si está al otro es hacia adentro. Cuando el propio punto O se encuentra en la recta soporte | ||
| + | |||
| + | <center><math>\overrightarrow{OP}\parallel \vec{F} \qquad\Rightarrow\qquad \vec{M}_O=\vec{0}</math></center> | ||
| + | |||
| + | Si tenemos varias fuerzas actuando sobre la misma partícula, la resultante de los momentos es igual al momento de la resultante | ||
| + | |||
| + | <center><math>\vec{M}_O=\sum_i \vec{M}_{iO}=\sum_i\vec{r}\times\vec{F}_i = \vec{r}\times\sum_i\vec{F}_i =\vec{r}\times\vec{F}</math></center> | ||
| + | |||
| + | ===Interpretación del momento cinético=== | ||
| + | Del mismo modo que la cantidad de movimiento, como su nombre indica, es una medida de cuánto se mueve una partícula (en el sentido de que, por ejemplo, en una colisión, importa tanto la velocidad del proyectil como su masa), el momento cinético mide la cantidad de rotación en torno al punto O. | ||
| + | |||
| + | Esto se ve claro en el caso de un movimiento circular. Si una partícula describe una circunferencia alrededor del punto O, el momento cinético respecto a este punto vale | ||
| + | |||
| + | <center><math>\vec{L}_O = m\vec{r}\times\vec{v}=m\vec{r}\times(\vec{\omega}\times\vec{r}) = mR^2\vec{\omega}</math></center> | ||
| + | |||
| + | Vemos que esta “cantidad de rotación” depende de con qué velocidad se gira, de la masa de la partícula y del radio de la circunferencia. | ||
| + | |||
| + | <center>[[Archivo:direccion-circulo.gif]]</center> | ||
| + | |||
| + | Esta idea se puede generalizar a movimientos no circulares. Si una partícula describe un movimiento rectilíneo y la observamos desde un punto exterior a la recta, nuestra dirección de observación va girando, aunque la partícula vaya en línea recta. Eso sí, cuanto mayor es la distancia, menor es el cambio de la dirección de observación. | ||
| + | |||
| + | <center>[[Archivo:direccion-recta.gif]]</center> | ||
| + | ===Cambio del centro de reducción=== | ||
| + | Si en vez de un punto O, calculamos el momento cinético respecto a otro punto fijo A | ||
| + | |||
| + | <center><math>\vec{L}_A = \overrightarrow{AP}\times\vec{p}</math></center> | ||
| + | |||
| + | la relación con el del punto O es | ||
| + | |||
| + | <center><math>\vec{L}_A=(\overrightarrow{AO}+\overrightarrow{OP})\times\vec{p}=\overrightarrow{AO}\times\vec{p}+\vec{L}_O</math></center> | ||
| + | |||
| + | siendo el vector <math>\overrightarrow{AO}</math> uno fijo, independiente del movimiento de la partícula. Invirtiendo el producto vectorial | ||
| + | |||
| + | <center><math>\vec{L}_A=\vec{L}_O+\vec{p}\times\overrightarrow{OA}</math></center> | ||
| + | |||
| + | Igualmente, para el momento de las fuerzas, tenemos que | ||
| + | |||
| + | <center><math>\vec{M}_A = \vec{M}_O+\vec{F}\times\overrightarrow{OA}</math></center> | ||
| + | |||
| + | siendo <math>\vec{F}</math> la resultante de las fuerzas aplicadas | ||
| + | |||
| + | ===Derivada del momento cinético (Teorema del momento cinético)=== | ||
| + | Como consecuencia de la segunda ley de Newton, la derivada del momento cinético de una partícula es igual al momento resultante sobre ella | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t} =m\left(\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right)\times\vec{v}+m\,\vec{r}\times\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=m\overbrace{\vec{v}\times\vec{v}}^{=\vec{0}}+\vec{r}\times\vec{F}=\vec{M}_O</math></center> | ||
| + | |||
| + | Para que esta expresión sea correcta, el punto O debe ser un punto fijo. | ||
| + | |||
| + | ===Teorema de conservación=== | ||
| + | De la expresión para la derivada del momento cinético se deduce su teorema de conservación: | ||
| + | |||
| + | :''Si la resultante de los momentos de las fuerzas que actúan sobre una partícula es nula, el momento cinético de dicha partícula permanece constante.'' | ||
| + | |||
| + | <center><math>\vec{0} = \vec{M}_O=\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}</math>{{tose}}<math>\vec{L}_O=\mathrm{cte}</math></center> | ||
| + | |||
| + | Una consecuencia inmediata de la conservación del momento cinético es: | ||
| + | |||
| + | :''La trayectoria de una partícula cuyo momento cinético permanece constante es plana.'' | ||
| + | |||
| + | El plano en el que ocurre la trayectoria es el definido por el centro de reducción, la posición inicial y la velocidad inicial. | ||
| + | |||
| + | Puesto que el momento cinético se conserva tenemos que si multiplicamos escalarmente el vector de posición relativo por este vector constante | ||
| + | |||
| + | <center><math> \vec{L}_O\cdot\vec{r}=m\overbrace{\left(\vec{r}\times\vec{v}\right)}^{\perp\vec{r}}\cdot\vec{r} = 0</math></center> | ||
| + | |||
| + | Esta es la ecuación vectorial de un plano que pasa por O y es normal a la dirección de <math>\vec{L}_O</math>. | ||
| + | |||
| + | ===Fuerzas centrales=== | ||
| + | Las fuerzas centrales constituyen un caso particular e importante de las diferentes fuerzas presentes en la naturaleza. Una ''fuerza central'' es aquella que en todos los puntos del espacio posee dirección radial desde un punto fijo O, siendo además dependiente solo de la distancia a dicho punto | ||
| + | |||
| + | <center><math>\vec{F}(\vec{r}) = f(|\vec{r}|)\vec{r}</math></center> | ||
| + | |||
| + | Ejemplos de fuerzas centrales son la fuerza de la gravedad debida a un objeto masivo (como la atracción que el Sol ejerce sobre la Tierra), o la fuerza eléctrica debida a una carga en reposo. | ||
| + | |||
| + | Se tiene que | ||
| + | |||
| + | :''El momento cinético respecto a un punto O de una partícula sometida a la acción de una fuerza central, con centro O, permanece constante.'' | ||
| + | |||
| + | La demostración es inmediata, ya que el vector de posición relativo y la fuerza son vectores paralelos | ||
| + | |||
| + | <center><math>\vec{M}_O = \vec{r}\times\overbrace{\vec{F}}^{\parallel\vec{r}} = \vec{0}\qquad\Rightarrow\qquad \vec{L}_O = \mathrm{cte}</math></center> | ||
| + | |||
| + | En particular, esto implica que la trayectoria de toda partícula sometida a una fuerza central (p.ej. una óirbita planetaria, o un oscilador armónico en 3 dimensiones) es una curva plana. | ||
| + | |||
| + | <!-- | ||
| + | ===Segunda ley de Kepler=== | ||
| + | [[Archivo:segunda-ley-kepler-planeta.gif|right]] | ||
| + | |||
| + | La segunda ley de Kepler fue formulada inicialmente para el movimiento planetario, pero se trata de una consecuencia general de la ley de conservación del momento cinético. | ||
| + | |||
| + | :''Una partícula cuyo momento cinético permanece constante barre áreas iguales en tiempos iguales'' | ||
| + | |||
| + | Aquí la velocidad con la que se “barren áreas” hay que entenderla empleando la '''velocidad areolar''': para una trayectoria plana se mide el ritmo con el que varía el área del triángulo mixtilíneo formado por el vector de posición inicial (medido desde el punto <math>O</math> respecto al cual se conserva el momento cinético), el vector de posición instantáneo, respecto al mismo origen, y el arco de trayectoria comprendido entre los dos puntos. | ||
| + | |||
| + | <center><math>V_A = \frac{\mathrm{d}A}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | Puesto que posee dimensiones de L²/T, no se trata realmente de una velocidad, sino de un ritmo de variación. | ||
| + | |||
| + | En forma vectorial, si <math>\vec{B}</math> es el vector perpendicular al plano que contiene a la trayectoria | ||
| + | |||
| + | <center><math>\vec{V}_A = \frac{\mathrm{d}A}{\mathrm{d}t}\vec{B} = \frac{\mathrm{d}\vec{A}}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | En un intervalo infinitesimal <math>\mathrm{d}t</math> el área barrida es la correspondiente a un triángulo que tiene por lados el vector de posición relativo, <math>\vec{r}</math>, y el desplazamiento diferencial | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{r} = \vec{r}(t+\mathrm{d}t)-\vec{r}(t)</math></center> | ||
| + | |||
| + | el área de este triángulo es | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{A}=\frac{1}{2}\vec{r}\times\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | y la velocidad areolar es igual a | ||
| + | |||
| + | <center><math>\vec{V}_A = \frac{\mathrm{d}\vec{A}}{\mathrm{d}t}=\frac{1}{2}\vec{r}\times\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\frac{\vec{L}_O}{2m}</math></center> | ||
| + | |||
| + | Por tanto, si el momento cinético permanece constante, la velocidad areolar también es una integral primera y tenemos la segunda ley de Kepler. | ||
| + | |||
| + | La consecuencia inmediata de este teorema es que un cuerpo sometido a una fuerza central, por ejemplo, un planeta, se mueve más rápidamente cuando se encuentra en las proximidades del centro de fuerzas que cuando se encuentra más alejado de él. | ||
| + | |||
| + | Para el caso de la órbita terrestre, podemos comprobar que en invierno, la distancia Tierra-Sol es menor que en verano, pues mientras entre el equinoccio de Otoño (23 de septiembre) y el de Primavera (21 de marzo) hay 179 días, entre el de Primavera y el de Otoño hay 184 días, esto es, el invierno es más corto que el verano, debido a la mayor proximidad. Concretamente, el perihelio (punto más próximo) es en torno al 4 de enero, mientras que el afelio (punto más alejado) es en torno al 4 de Julio. | ||
| + | |||
| + | Este resultado también es aplicable al caso de una trayectoria abierta, incluyendo ahí el caso particular de un movimiento rectilíneo uniforme. | ||
| + | |||
| + | ===Expresión en coordenadas polares=== | ||
| + | El teorema del momento cinético presenta una expresión extremadamente sencilla en el caso de una partícula que efectúa un movimiento plano, si se emplean coordenadas polares. | ||
| + | |||
| + | Para un movimiento plano, el vector de posición de una partícula es | ||
| + | |||
| + | <center><math>\vec{r}=\rho\vec{u}_\rho</math></center> | ||
| + | |||
| + | y su velocidad | ||
| + | |||
| + | <center><math>\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\varphi}\vec{u}_\varphi</math></center> | ||
| + | |||
| + | Multiplicando vectorialmente estas dos cantidades obtenemos la velocidad areolar y el momento cinético respecto al origen de coordenadas | ||
| + | |||
| + | <center><math>\vec{V}_A=\frac{\rho^2\dot{\varphi}}{2}\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{L}=m\rho^2\dot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | La derivada temporal de esta expresión nos da | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}(\rho^2\dot{\varphi})=M_z</math></center> | ||
| + | |||
| + | En el caso de una fuerza central, esta se expresa en polares | ||
| + | |||
| + | <center><math>\vec{F}=F(\rho)\vec{u}_\rho</math></center> | ||
| + | |||
| + | y la ecuación de movimiento correspondiente | ||
| + | |||
| + | <center><math>\ddot{\rho}-\rho\dot{\varphi}^2=\frac{1}{m}F(\rho)</math>{{qquad}}{{qquad}}<math>\rho\ddot{\varphi}+2\dot{\rho}\dot{\varphi}=0</math></center> | ||
| + | |||
| + | La segunda ecuación es equivalente a la ley de conservación del momento cinético | ||
| + | |||
| + | <center><math>\rho^2\dot{\varphi}=\frac{L_0}{m}</math></center> | ||
| + | |||
| + | Despejando de aquí y sustituyendo en la componente radial de la aceleración queda | ||
| + | |||
| + | <center><math>\ddot{\rho}=\frac{L_0^2}{m^2\rho^3}+F(\rho)</math></center> | ||
| + | |||
| + | que matemáticamente es equivalente a una ecuación de movimiento rectilíneo, con un término de fuerza adicional. | ||
| + | --> | ||
| + | <!-- | ||
| + | ===Conservación parcial del momento cinético=== | ||
| + | Existen ocasiones en que el momento cinético no se conserva. Sin embargo, incluso en esos casos es a menudo posible obtener una ley de conservación más restringida. | ||
| + | |||
| + | Para ello, tenemos en cuenta que el momento cinético es un vector y posee tres componentes. Puede ocurrir que aunque el vector como tal no sea constante, una de sus componentes sí lo sea. Sea <math>\vec{u}</math> un vector unitario fijo. La componente del momento angular según la dirección de <math>\vec{u}</math> es | ||
| + | |||
| + | <center><math>L_{u}=\vec{L}_O\cdot\vec{u}\,</math></center> | ||
| + | |||
| + | Derivando aquí respecto al tiempo | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}L_u}{\mathrm{d}t}=\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\cdot\vec{u}=\vec{M}_O\cdot\vec{u}=M_u</math></center> | ||
| + | |||
| + | Si se anula la componente en la dirección de <math>\vec{u}</math> del momento de las fuerzas aplicadas, la componente del momento cinético en dicha dirección permanece constante. | ||
| + | --> | ||
| + | |||
| + | ===Ejemplo. Péndulo simple=== | ||
| + | Un ejemplo de aplicación del teorema del momento cinético en el que se simplifican los cálculos respecto a la aplicación directa de las leyes de Newton es el caso del [[Aplicaciones_de_las_leyes_de_Newton_(GIE)#Oscilaciones_no_lineales._P.C3.A9ndulo_simple|péndulo simple]]. | ||
| + | |||
| + | Supongamos una partícula de masa <math>m</math> atada a un hilo inextensible que por su otro extremo está atado a un punto de anclaje fijo O. | ||
| + | |||
| + | <center>[[Archivo:fuerzas-pendulo-02.png]]</center> | ||
| + | |||
| + | Tal como se ve en el apartado correspondiente de aplicaciones de las leyes de Newton, la masa se encuentra sometida a la acción conjunto de dos fuerzas: el peso y la tensión del hilo, de forma que | ||
| + | |||
| + | <center><math>m\vec{a}=m\vec{g}+\vec{F}_T</math></center> | ||
| + | |||
| + | Desarrollando esta ecuación en sus componentes y eliminando la tensión entre las dos ecuaciones que resultan se llega a la ecuación del péndulo | ||
| + | |||
| + | <center><math>\ddot{\theta}=-\frac{g}{l}\mathrm{sen}(\theta)</math></center> | ||
| + | |||
| + | la complicación que tiene este método es que obliga a introducir la tensión, que es una fuerza desconocida ''a priori''. | ||
| + | |||
| + | Veamos como sería con ayuda del momento cinético. El momento cinético respecto al punto O es igual a | ||
| + | |||
| + | <center><math>\vec{L}_O=m\vec{r}\times\vec{v}</math></center> | ||
| + | |||
| + | donde | ||
| + | |||
| + | <center><math>\vec{r}=l\vec{u}_\rho\qquad \vec{v}=l\dot{\varphi}\vec{u}_\varphi</math></center> | ||
| + | |||
| + | Al ser perpendiculares estos dos vectores, su producto vectorial es igual a | ||
| + | |||
| + | <center><math>\vec{L}_O=ml^2\dot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | siendo <math>\vec{k}</math> el vector normal hacia afuera del plano de oscilación del péndulo (no el de la dirección de la gravedad, que en estos ejes sería <math>\vec{g}=g\vec{\imath}</math>). La derivada respecto al tiempo del momento cinético es | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=ml^2\ddot{\varphi}\vec{k}</math></center> | ||
| + | |||
| + | Esta derivada debe ser igual a la resultante de los momento de las fuerzas aplicadas | ||
| + | |||
| + | <center><math>\vec{M}_O=\vec{r}\times\vec{F}_T+\vec{r}\times(m\vec{g})</math></center> | ||
| + | |||
| + | Ahora bien, la tensión va en la dirección del hilo, que es también la del vector de posición. Por tanto, su momento es nulo y solo queda el del peso. Éste, a su vez, es igual a la distancia a la recta soporte (la vertical que pasa por la partícula), con lo que su momento vale | ||
| + | |||
| + | <center><math>\vec{M}_O=-x(mg)\vec{k} = -mgl\,\mathrm{sen}(\varphi)\vec{k}</math></center> | ||
| + | |||
| + | el signo negativo viene de que cuando <math>\varphi</math> es positivo, la regla de la mano derecha da para el momento un sentido hacia adentro del plano. | ||
| + | |||
| + | Igualando las dos cantidades queda | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}=\vec{M}_O\qquad\Rightarrow\qquad ml^2\ddot{\varphi}=-mgl\,\mathrm{sen}(\varphi)\qquad\Rightarrow\qquad \ddot{\varphi}=-\frac{g}{l}\mathrm{sen}(\varphi)</math></center> | ||
| + | |||
| + | ==Trabajo y energía cinética== | ||
| + | ===Trabajo de una fuerza constante=== | ||
| + | Cuando una fuerza constante se aplica sobre un cuerpo que realiza un desplazamiento <math>\Delta x</math> en la dirección de la fuerza aplicada, se dice que la fuerza realiza un trabajo | ||
| + | |||
| + | <center><math>W = F\,\Delta x</math></center> | ||
| + | |||
| + | Vemos que las unidades en las que se mide el trabajo son las de una fuerza por una distancia, siendo la unidad SI 1 julio = 1 newton·m. | ||
| + | |||
| + | El trabajo es positivo si la fuerza se aplica en el mismo sentido que se realiza el desplazamiento y negativo si se opone a él. El trabajo es nulo si no hay desplazamiento. Una persona puede ejercer toda la fuerza que quiera contra una pared, hasta agotarse. Si la pared no se mueve, no ha realizado trabajo alguno. | ||
| + | |||
| + | Si la fuerza, como vector que es, posee una dirección diferente al desplazamiento, solo su componente en la dirección de este realiza trabajo | ||
| + | |||
| + | <center><math>W = F_\parallel\,\Delta x</math></center> | ||
| + | |||
| + | Esta cantidad de expresa de manera más sencilla con ayuda del producto escalar | ||
| + | |||
| + | <center><math>W = \vec{F}\cdot\Delta\vec{r}</math></center> | ||
| + | |||
| + | Vemos que | ||
| + | |||
| + | * El trabajo es una cantidad escalar, con signo. | ||
| + | * No se realiza trabajo si se ejerce una fuerza pero no se produce desplazamiento. | ||
| + | * Una fuerza perpendicular al desplazamiento no realiza trabajo alguno. | ||
| + | |||
| + | ===Trabajo de una fuerza variable=== | ||
| + | [[Archivo:trabajo-rectificado.png|right]] | ||
| + | |||
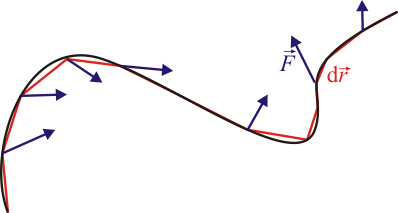
| + | Si tenemos una partícula que realiza una trayectoria arbitraria, sometida a una fuerza variable con la posición o el tiempo, podemos hallar el trabajo dividiendo el camino en diferenciales casi rectilíneos, calculando el trabajo (diferencial) en cada uno, y sumando (integrando) el resultado. | ||
| + | |||
| + | El trabajo diferencial es igual a | ||
| + | <center><math>\delta{}W=\vec{F}\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | A partir de aquí obtenemos el trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C como la suma de los trabajos elementales a lo largo de dicha curva | ||
| + | |||
| + | <center><math>W_{A\to B} = \int_{\!\!\!\!\!\!\!\!\! C\ A}^B \delta W = \int_{\!\!\!\!\!\!\!\!\! C\ A}^B \vec{F}\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | Respecto a la notación, el hecho de que el trabajo diferencial (que no diferencial de trabajo) se represente como <math>\delta W</math> en lugar de <math>\mathrm{d}W</math> se debe justamente al hecho de que es una cantidad que depende del camino, como se estudia en más detalle en [[Trabajo_en_termodinámica_(GIE)|Termodinámica]]. | ||
| + | |||
| + | ===Trabajo de la superposición de varias fuerzas=== | ||
| + | Si sobre una partícula actúan varias fuerzas simultáneamente, por el principio de superposición, el trabajo total será igual a la suma de los trabajos individuales | ||
| + | |||
| + | <center><math>W_i = \int_{\!\!\!\!\!\!\!\!\! C\ A}^B \vec{F}_i\cdot\mathrm{d}\vec{r}\qquad\qquad\vec{F}=\sum_i\vec{F}_i\qquad W = \sum_i W_i</math></center> | ||
| + | |||
| + | ===Potencia=== | ||
| + | A partir del trabajo, se define la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo <math>\mathrm{d}t</math>, dividido por dicho intervalo | ||
| + | |||
| + | <center><math>P = \frac{\delta{}W}{\mathrm{d}t}=\vec{F}\cdot\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\vec{F}\cdot\vec{v}</math></center> | ||
| + | |||
| + | De esta definición resulta que la potencia tiene dimensiones de trabajo partido por tiempo (o fuerza multiplicada por velocidad), siendo su unidad el vatio (W), igual a un 1 J/s. | ||
| + | |||
| + | ===Energía cinética. Teorema de la fuerzas vivas=== | ||
| + | ====Caso de una fuerza constante==== | ||
| + | En el caso de una partícula sometida a una fuerza neta constante, el resultado es un movimiento con aceleración constante. | ||
| + | |||
| + | <center><math>\vec{r}=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{a}t^2\qquad \vec{v}=\vec{v}_0+\vec{a}t</math></center> | ||
| + | |||
| + | Si multiplicamos escalarmente la segunda ecuación por sí misma nos queda | ||
| + | |||
| + | <center><math>|\vec{v}|^2 = (\vec{v}_0+\vec{a}t)\cdot(\vec{v}_0+\vec{a}t) = |\vec{v}_0|^2+2\vec{a}\cdot\left(\vec{v}_0t+\frac{1}{2}\vec{a}t^2\right)</math></center> | ||
| + | |||
| + | y teniendo en cuenta el desplazamiento dado por la ecuación horaria nos queda | ||
| + | |||
| + | <center><math>|\vec{v}|^2=|\vec{v}_0|^2 + 2\vec{a}\cdot\Delta\vec{r}</math></center> | ||
| + | |||
| + | Multiplicando por la masa y dividiendo por 2 nos queda finalmente | ||
| + | |||
| + | <center><math>\frac{1}{2}m|\vec{v}|^2 -\frac{1}{2}m|\vec{v}_0|^2 = (m\vec{a})\cdot\Delta\vec{r}=\vec{F}\cdot\Delta \vec{r} = W</math></center> | ||
| + | |||
| + | que podemos abreviar como | ||
| + | |||
| + | <center><math>\Delta K=W\,</math></center> | ||
| + | |||
| + | siendo <math>K</math> una cantidad que llamamos ''energía cinética'' de la partícula | ||
| + | |||
| + | <center><math>K = \frac{1}{2}m|\vec{v}|^2</math></center> | ||
| + | |||
| + | ====Caso de una fuerza variable==== | ||
| + | Si tenemos una trayectoria arbitraria que va del punto A al punto B y la partícula está sometida a una fuerza neta variable, simplemente dividimos el camino en pequeñas porciones en cada una de las cuales puede suponerse la fuerza prácticamente constante. Para cada uno de estos diferenciales de camino se cumplirá | ||
| + | |||
| + | <center><math>\mathrm{d}K = \mathrm{d}\left(\frac{1}{2}m|\vec{v}|^2\right) = \vec{F}\cdot\mathrm{d}\vec{r} = \delta{}W</math></center> | ||
| + | |||
| + | y sumando para todas las porciones obtenemos la relación | ||
| + | <center><math> | ||
| + | \int_A^B \mathrm{d}K = \int_{\!\!\!\!\!\!\!\!\! C\ A}^B \delta{}W \qquad \rightarrow\qquad \Delta K = W_{A\to B}</math></center> | ||
| + | |||
| + | La identidad | ||
| + | |||
| + | <center><math>W_{A\to B} = \Delta K\,</math></center> | ||
| + | |||
| + | se conoce como ''teorema de las fuerzas vivas'' (o ''teorema trabajo-energía cinética''). | ||
| + | |||
| + | ====Interpretación==== | ||
| + | El teorema de las fuerzas vivas | ||
| + | |||
| + | <center><math>W_{A\to B} = K(B)-K(A)\,</math></center> | ||
| + | |||
| + | requiere una cierta interpretación ya que se presta a confusiones. Lo enunciamos primero con palabras: | ||
| + | |||
| + | :''El trabajo realizado entre dos puntos por la resultante de las fuerzas que actúan sobre una partícula es igual al incremento de la energía cinética entre dichos dos puntos'' | ||
| + | |||
| + | Es decir, si se hace un trabajo positivo sobre la partícula, su energía cinética aumenta, esto es, se mueve más rápido. Si por contra el trabajo es negativo, oponiéndose al movimiento, la energía cinética disminuye y la partícula se mueve más despacio. | ||
| + | |||
| + | Si la partícula tiene en el punto B la misma rapidez que en el punto A, su energía cinética no ha cambiado y por tanto el trabajo neto realizado sobre ella es nulo, independientemente de que haya existido una fuerza actuando sobre ella, acelerándola en los puntos intermedios. | ||
| + | |||
| + | Hay que remarcar que el teorema de las fuerzas vivas habla de la fuerza neta, esto es, la resultante de las fuerzas aplicadas. Si sobre una partícula actúan varias fuerzas simultáneamente, cada una de ellas realizará un trabajo, pero cada uno de ellos no es igual a la variación de la energía cinética, solo su suma lo es. | ||
| + | |||
| + | <center><math>\vec{F}=\sum_i \vec{F}_i\qquad\rightarrow\qquad W = \sum_i W_i = \Delta K\,</math></center> | ||
| + | |||
| + | También hay que remarcar otro aspecto de la expresión del teorema. Puede aparecer extraño que de la relación | ||
| + | |||
| + | <center><math>\mathrm{d}K = \delta{}W\,</math></center> | ||
| + | |||
| + | no se deduzca la igualdad entre dos incrementos. La razón es profunda y se relaciona con conceptos más generales que se estudian en [[Trabajo_en_termodinámica_(GIE)|Termodinámica]]. La idea es la siguiente: | ||
| + | |||
| + | * La energía cinética es una ''función de estado'': esto quiere decir que conocido el estado de la partícula (su posición y su velocidad instantáneas), podemos hallar su energía cinética | ||
| + | |||
| + | <center><math>K = \frac{1}{2}m|\vec{v}|^2</math></center> | ||
| + | |||
| + | :y su valor es uno solo. Podemos imaginar que la partícula, por moverse con la rapidez que lo hace, almacena una cierta cantidad de energía cinética. Por ello, el incremento de K es igual a su valor en B menos su valor en A. | ||
| + | |||
| + | * El trabajo no es una función de estado, sino que ''depende del camino'': no nos basta con saber qué posición y que velocidad tiene la partícula en un momento dado, sino que necesitamos saber qué curva ha descrito (por ello se indica una C en la integral correspondiente) y qué fuerza ha actuado sobre ella en cada punto del camino. El trabajo es por sí mismo una integral. No es el incremento ni la variación de nada. No podemos decir que la partícula almacena un trabajo. | ||
| + | |||
| + | Por ello, los dos diferenciales anteriores son de distinto tipo y se representan con letras diferentes, el de la energía con <math>\mathrm{d}</math> y el del trabajo con <math>\delta</math>. El diferencial de energía es un incremento muy pequeño de una función. El trabajo diferencial es una cantidad muy pequeña de trabajo realizado. | ||
| + | |||
| + | Así, el teorema de las fuerzas vivas representa que un trabajo realizado sobre una partícula se “almacena” en forma de energía cinética. | ||
| + | |||
| + | ====Forma diferencial del teorema==== | ||
| + | A partir de la relación entre los diferenciales podemos escribir el teorema de las fuerzas vivas como una relación entre derivadas en lugar de integrales. | ||
| + | |||
| + | <center><math>\mathrm{d}K = \vec{F}\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | Dividiendo por el diferencial de tiempo empleado en realizar el desplazamiento | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}K}{\mathrm{d}t} = \vec{F}\cdot\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\vec{F}\cdot\vec{v}=P</math></center> | ||
| + | |||
| + | esto es, en cada instante, la derivada respecto al tiempo de la energía cinética es igual a la potencia neta realizada sobre la partícula. | ||
| + | |||
| + | ====Aplicación a colisiones==== | ||
| + | Cuando se produce una colisión, una partícula experimenta una fuerza muy intensa durante un periodo de tiempo muy corto. Esta fuerza es capaz de producir un cambio neto en la cantidad de movimiento (el impulso). También puede producir un incremento en la energía cinética | ||
| + | |||
| + | <center><math>\Delta K=\int_{t_0}^{t_0+\epsilon}\vec{F}\cdot\vec{v}\,\mathrm{d}t</math></center> | ||
| + | |||
| + | Así, en el caso de una colisión oblicua contra una [[Cantidad_de_movimiento_y_momento_cinético_(GIE)#Pared_estacionaria|pared estacionaria]] en <math>z=0</math> tenemos las velocidades antes y después del choque | ||
| + | |||
| + | <center><math>\vec{v}_i=v_{x0}\vec{\imath}+v_{z0}\vec{k}\qquad\qquad \vec{v}_f=v_{x0}\vec{\imath}-v_{z0}\vec{k}</math></center> | ||
| + | |||
| + | y por tanto el incremento de la energía cinética en este caso es nulo | ||
| + | |||
| + | <center><math>\Delta K = \frac{1}{2}m\left(v_{x0}^2+v_{z0}^2\right)-\frac{1}{2}m\left(v_{x0}^2+v_{z0}^2\right)=0</math></center> | ||
| + | |||
| + | Por ello se dice que tenemos una colisión elástica. | ||
| + | |||
| + | En el caso de un choque frontal contra una [[Cantidad_de_movimiento_y_momento_cinético_(GIE)#Pared_en_movimiento|pared en movimiento]] las velocidades inicial y final valen | ||
| + | |||
| + | <center><math>\vec{v}_i=v_0\vec{\imath}\qquad\qquad \vec{v}_f = (2V-v_0)\vec{\imath}</math></center> | ||
| + | |||
| + | por lo que resulta un incremento de energía cinética que no será nulo en general | ||
| + | |||
| + | <center><math>\Delta K = \frac{1}{2}m(2V-v_0)^2-\frac{1}{2}mv_0^2 = 2mV(V-v_0)</math></center> | ||
| + | |||
| + | Se anulará si la pared está en reposo (caso anterior) o si la partícula se mueve con la misma velocidad que la pared (con lo que no llegan a chocar). | ||
| + | |||
| + | ===Teorema de conservación de la energía cinética=== | ||
| + | Este teorema implica, entre otras resultados, que | ||
| + | |||
| + | :“''Una partícula sometida a una fuerza puramente normal a su trayectoria (o nula) en todo momento mantiene constante su energía cinética y por tanto se mueve de manera uniforme (aunque la dirección de movimiento sea cambiante).''” | ||
| + | |||
| + | Ejemplo de fuerzas permanentemente normales a la trayectoria son: | ||
| + | * La fuerza magnética <math>\vec{F}_m = q\vec{v}\times\vec{B}</math> | ||
| + | * La fuerza de Coriolis que aparece en sistemas no inerciales. | ||
| + | * Las fuerzas de reacción vincular debidas a vínculos sin rozamiento e independientes del tiempo. | ||
| + | |||
| + | Esta última propiedad es especialmente importante porque permite aplicar el teorema de conservación de la energía mecánica a partículas vinculadas, sin necesidad de considerar las fuerzas de reacción a la hora de calcular la energía. Por ejemplo, puede hallarse la velocidad de una masa que desciende por un plano inclinado empleando razonamientos energéticos sin incluir la reacción normal al plano. | ||
| + | |||
| + | ===Ejemplos=== | ||
| + | ====Trabajo debido al peso==== | ||
| + | El peso de un cuerpo es una fuerza constante, por lo que se aplica directamente el resultado anterior, sin necesidad de hacer integral alguna | ||
| + | |||
| + | <center><math>W = \vec{F}\cdot\Delta \vec{r} = -mg\vec{k}\cdot\Delta r</math></center> | ||
| + | |||
| + | Teniendo en cuenta la expresión del vector de posición en cartesianas | ||
| + | |||
| + | <center><math>\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}</math></center> | ||
| + | |||
| + | nos queda, para el trabajo | ||
| + | |||
| + | <center><math>W = -mg\,\Delta z = mg(z_i-z_f)\,</math></center> | ||
| + | |||
| + | Este trabajo es igual al aumento de la energía cinética | ||
| + | |||
| + | <center><math>\Delta K = \frac{1}{2}m|\vec{v}_f|^2- \frac{1}{2}m|\vec{v}_i|^2</math></center> | ||
| + | |||
| + | Igualando ambas cantidades | ||
| + | |||
| + | <center><math>\frac{1}{2}m|\vec{v}_f|^2- \frac{1}{2}m|\vec{v}_i|^2 = mg(z_i-z_f)</math></center> | ||
| + | |||
| + | En el caso particular de un objeto que cae desde una altura h, partiendo del reposo, y llega hasta el suelo | ||
| + | |||
| + | <center><math>\frac{1}{2}m|\vec{v}_f|^2- \frac{1}{2}m\overbrace{|\vec{v}_i|^2}^{=0} = mg(\overbrace{z_i}^{=h}-\overbrace{z_f}^{=0})</math></center> | ||
| + | |||
| + | Nos queda, para la rapidez de impacto | ||
| + | |||
| + | <center><math>\frac{1}{2}m|\vec{v}_f|^2 = mgh\qquad\Rightarrow\qquad |\vec{v}_f| = \sqrt{2gh}</math></center> | ||
| + | |||
| + | Obsérvese que el resultado es independiente de que el objeto caiga verticalmente o describiendo una parábola. | ||
| + | |||
| + | ====Trabajo de un oscilador armónico==== | ||
| + | El teorema de las fuerzas vivas posee numerosas aplicaciones, ya que permite determinar celeridades sin necesidad de resolver la ecuación de movimiento. | ||
| + | |||
| + | Consideremos el caso de un oscilador armónico que se libera desde el reposo a una distancia A del punto de equilibrio. ¿Que rapidez tiene la masa cuando pasa por éste? ¿Qué trabajo se realiza entre el punto inicial y el de máxima elongación al otro lado de la posición de equilibrio? | ||
| + | |||
| + | El trabajo que realiza la fuerza recuperadora entre la posición inicial y la de equilibrio vale | ||
| + | |||
| + | <center><math>\vec{F}=-kx \vec{\imath}\qquad \mathrm{d}\vec{r}=\mathrm{d}x\vec{\imath}\qquad\Rightarrow\qquad W=\int_A^0(-kx\vec{\imath})\cdot(\mathrm{d}x\vec{\imath})=-k\int_A^0x\,\mathrm{d}x=\frac{kA^2}{2}</math></center> | ||
| + | |||
| + | Este trabajo es igual al incremento de energía cinética | ||
| + | |||
| + | <center><math>\frac{1}{2}kA^2 = \Delta K = \frac{1}{2}m|\vec{v}(x=0)|^2-\frac{1}{2}m\overbrace{|\vec{v}(x=A)|^2}^{=0}\qquad\Rightarrow\qquad |\vec{v}(x=0)| = \sqrt{\frac{k}{m}}A</math></center> | ||
| + | |||
| + | vemos que hallamos la rapidez en el punto de equilibrio sin necesidad de usar los senos y cosenos que nos dan las ecuaciones horarias. | ||
| + | |||
| + | Para la segunda cuestión, el trabajo realizado entre el punto inicial (de velocidad nula) y el punto opuesto de máxima elongación (que también es un punto de reposo instantáneo) es nulo. | ||
| + | |||
| + | <center><math>W= \Delta K = \frac{1}{2}m\overbrace{|\vec{v}(x=-A)|^2}^{=0}-\frac{1}{2}m\overbrace{|\vec{v}(x=A)|^2}^{=0} = 0</math></center> | ||
| + | |||
| + | ====Partícula que desliza por un aro==== | ||
| + | Sea una pequeña anilla de masa <math>m</math> ensartada en un aro circular de radio <math>R</math> puesto verticalmente. Si la anilla se suelta desde el reposo en el punto más alto del aro y el rozamiento es despreciable, ¿con qué velocidad llega al punto más bajo? | ||
| + | |||
| + | La partícula está sometida a dos fuerzas, su peso y la fuerza de reacción del aro. | ||
| + | |||
| + | <center><math>\vec{F} = m\vec{g}+\vec{F}_n</math></center> | ||
| + | |||
| + | El trabajo total realizado sobre la partícula será la suma de los dos trabajos individuales | ||
| + | |||
| + | <center><math>W = \int_{\vec{r}_0}^{\vec{r}_1}m\vec{g}\cdot\mathrm{d}\vec{r}+\int_{\vec{r}_0}^{\vec{r}_1}\vec{F}_n\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | El trabajo de la fuerza de reacción es nulo, ya que la fuerza es perpendicular en todo momento al desplazamiento | ||
| + | |||
| + | <center><math>\vec{F}_n\cdot\mathrm{d}\vec{r}= 0\qquad\Rightarrow\qquad \int_{\vec{r}_0}^{\vec{r}_1}\vec{F}_n\cdot\mathrm{d}\vec{r}=0</math></center> | ||
| + | |||
| + | El trabajo debido al peso se halla, como antes, observando que se trata de una fuerza constante (o bien, explícitamente por la integral, como en un [[Trabajo_en_una_semicircunferencia|problema]]) y el resultado es | ||
| + | |||
| + | <center><math>W = 2mgR\,</math></center> | ||
| + | |||
| + | Esto nos da la rapidez final | ||
| + | |||
| + | <center><math>\frac{1}{2}m|\vec{v}|^2 -\frac{1}{2}m\overbrace{|\vec{v}_0|^2}^{=0}=2mgR\qquad\Rightarrow\qquad |\vec{v}| = \sqrt{4gR}</math></center> | ||
| + | |||
| + | Obsérvese que aunque la fuerza de reacción no realice trabajo sí que acelera a la partícula, cambiando su dirección de movimiento. Si solo actuara el peso, la anilla caería verticalmente. Es la fuerza de reacción la que hace en el punto más bajo la velocidad sea horizontal. | ||
| + | |||
| + | ====Disipación de energía cinética==== | ||
| + | En el caso de una partícula sometida exclusivamente a una fuerza de rozamiento dinámico (seco o viscoso), la energía cinética disminuye de forma continuada, ya que | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}K}{\mathrm{d}t}=\vec{F}_r\cdot\vec{v}</math></center> | ||
| + | |||
| + | Dado que la fuerza de rozamiento dinámico se opone a la velocidad, este producto escalar es negativo y la energía cinética disminuye. | ||
| + | |||
| + | En particular, en el caso de un rozamiento viscoso lineal nos queda | ||
| + | |||
| + | <center><math>\vec{F}_r = -\gamma\vec{v}\qquad \frac{\mathrm{d}K}{\mathrm{d}t}=-\gamma |\vec{v}|^2 = -\frac{2\gamma}{m}K</math></center> | ||
| + | |||
| + | Separando diferenciales e integrando llegamos a un decaimiento exponencial en la energía cinética | ||
| + | |||
| + | <center><math>K(t) = K_0\mathrm{e}^{-t/\tau}\qquad \tau = \frac{m}{2\gamma}</math></center> | ||
| + | |||
| + | El tiempo que tarda la energía en disiparse es independiente de la velocidad inicial. Sí depende de la masa de la partícula. Cuanto mayor sea su masa, y por tanto su inercia, más lentamente decae la energía. | ||
| + | |||
| + | ==Energía potencial== | ||
| + | ===Definición=== | ||
| + | El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos. | ||
| + | |||
| + | Existe una clase de fuerzas, denominadas '''fuerzas conservativas''', para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro | ||
| + | |||
| + | [[Archivo:Caminos-U.png|right]] | ||
| + | |||
| + | <center><math>W_{A\to B}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_1\ A}^B \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}=\int_{\!\!\!\!\!\!\!\!\!\!\!\! C_2\ A}^B \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | [[Archivo:Caminos-U-01.png|left]] | ||
| + | |||
| + | Esto permite definir una función denominada ''energía potencial'' como el trabajo, cambiado de signo, para ir desde un punto fijo O (el ''origen de potencial'') hasta un punto fijo | ||
| + | |||
| + | <center><math>U(P)=-\int_{O}^P \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}\,</math></center> | ||
| + | |||
| + | Entre los casos importantes de fuerzas conservativas tenemos: | ||
| + | |||
| + | * El peso, para el cual, si el origen de potencial es la superficie terrestre y <math>z</math> la altura sobre ella: | ||
| + | |||
| + | <center><math>U(\vec{r}) = mg z\,</math></center> | ||
| + | |||
| + | * Más en general la fuerza gravitatoria producida por un cuerpo fijo sobre otro, tomando como origen de potencial el infinito, tiene una energía potencial | ||
| + | |||
| + | <center><math>U(\vec{r}) = -\frac{GMm}{|\vec{r}|}\,</math></center> | ||
| + | |||
| + | * El oscilador armónico, que cumple la ley de Hooke, tomando el origen de potencial en el punto de equilibrio, tiene una energía potencial, en el caso rectilíneo | ||
| + | |||
| + | <center><math>U(x) = \frac{1}{2}kx^2</math></center> | ||
| + | |||
| + | :y en el caso general | ||
| + | |||
| + | <center><math>U(\vec{r}) = \frac{1}{2}k|\vec{r}|^2\,</math></center> | ||
| + | |||
| + | La energía potencial se obtiene a partir de la fuerza, integrando respecto a la posición. Para ello hay que elegir un camino (que es arbitrario, pero uno hay que elegir) que lleve del origen de potencial al punto donde queremos hallar el potencial. | ||
| + | |||
| + | En el caso de una fuerza dependiente de la posición a lo largo de una recta que actúa sobre una partícula que se mueve sobre esta recta, el camino es inmediato: es la propia recta de movimiento | ||
| + | |||
| + | <center><math>\vec{F}=F(x)\vec{\imath}\qquad\qquad \vec{r}=x\vec{\imath}\qquad\qquad \mathrm{d}\vec{r}=\mathrm{d}x\,\vec{\imath}</math></center> | ||
| + | |||
| + | y la integral de camino se reduce a una integral usual | ||
| + | |||
| + | <center><math>U(x) =-\int_{x_0}^x F(x)\,\mathrm{d}x</math></center> | ||
| + | |||
| + | Así, para el caso del oscilador armónico, tomando como origen de potencial la posición de equilibrio | ||
| + | |||
| + | <center><math>F(x) = -kx\qquad\Rightarrow\qquad U(x) = -\int_0^x (-kx)\mathrm{d}x=\frac{1}{2}kx^2</math></center> | ||
| + | |||
| + | En tres dimensiones el problema es más complicado, aunque para fuerzas centrales podemos tomar un camino rectilíneo radial | ||
| + | |||
| + | <center><math>\vec{F}=F(r)\vec{u}_r\qquad\qquad\mathrm{d}\vec{r}=\mathrm{d}r\vec{u}_r\qquad\qquad(r = |\vec{r}|)</math></center> | ||
| + | |||
| + | y para el oscilador armónico en tres dimensiones resulta | ||
| + | |||
| + | <center><math>U(\vec{r})=-\int_0^r (-k\vec{r})\cdot(\mathrm{d}r\,\vec{u}_r)=\int_0^r kr\,\mathrm{d}r=\frac{1}{2}kr^2=\frac{1}{2}k|\vec{r}|^2</math></center> | ||
| + | |||
| + | De manera similar se calcula la energía potencial gravitatoria. | ||
| + | |||
| + | Inversamente, se puede hallar la fuerza, conocida la energía potencial, derivando respecto a la posición. | ||
| + | |||
| + | En el caso de un movimiento rectilíneo la energía potencial depende solo de una variable, <math>x</math>, y la fuerza es igual a | ||
| + | |||
| + | <center><math>F(x) = -\frac{\mathrm{d}U}{\mathrm{d}x}</math></center> | ||
| + | |||
| + | En el caso general del movimiento tridimensional, una fuerza conservativa se calcula a partir de la energía potencial hallando el ''gradiente'': | ||
| + | |||
| + | <center><math>\vec{F}=-\nabla U = -\frac{\partial U}{\partial x}\vec{\imath}-\frac{\partial U}{\partial y}\vec{\jmath}-\frac{\partial U}{\partial z}\vec{k}</math></center> | ||
| + | |||
| + | donde las derivadas son parciales, esto es, calculadas derivando respecto a una coordenada tratando al resto de coordenadas como constantes. | ||
| + | |||
| + | Por ejemplo, para la energía potencial de un oscilador armónico, en el caso rectilíneo | ||
| + | |||
| + | <center><math>U(x) = \frac{1}{2}kx^2\qquad \Rightarrow\qquad F = -\frac{\mathrm{d}U}{\mathrm{d}x}=-kx</math></center> | ||
| + | |||
| + | En tres dimensiones | ||
| + | |||
| + | <center><math>U(\vec{r}) = \frac{1}{2}k|\vec{r}|^2 = \frac{k}{2}(x^2+y^2+z^2)</math></center> | ||
| + | |||
| + | hallando las tres derivadas parciales obtenemos la fuerza | ||
| + | |||
| + | <center><math>\vec{F}=-kx\vec{\imath}-ky\vec{\jmath}-kz\vec{k}=-k\vec{r}</math></center> | ||
| + | |||
| + | ===Trabajo y energía potencial=== | ||
| + | Con la definición de energía potencial se cumple, para fuerzas conservativas, | ||
| + | |||
| + | <center><math>W_{A\to B}=U(A) - U(B) = -\Delta U\,</math></center> | ||
| + | |||
| + | La demostración es la siguiente. Debemos hallar el trabajo en el camino de A a B. Si <math>\vec{F}</math> es conservativa, podemos elegir el camino que queramos para ir de un punto a otro. Tomamos entonces una ruta que pasa por O. | ||
| + | |||
| + | <center>[[Archivo:Caminos-U-02.png]]</center> | ||
| + | |||
| + | Entonces se cumple | ||
| + | |||
| + | <center><math>W_{A\to B}=\int_A^B \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}=\int_A^O \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}\ +\int_O^B \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}=-\int_O^A \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}\ +\int_O^B \vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r} = U(A)-U(B) = -\Delta U</math></center> | ||
| + | |||
| + | La identidad anterior es similar al teorema de las fuerzas vivas, con dos diferencias importantes: | ||
| + | |||
| + | * Solo se aplica a fuerzas conservativas, no a todas las fuerzas (en particular, no al rozamiento). | ||
| + | * Nos habla de lo que ocurre de una fuerza ''individual''. En una partícula sometida a varias fuerzas, cada una podrá o no derivar de una energía potencial. El teorema de las fuerzas vivas habla de la ''resultante'' de todas las fuerzas aplicadas. | ||
| + | * Hay un signo menos, con lo que el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial. | ||
| + | |||
| + | Podemos interpretar entonces el resultado diciendo que la partícula por estar sometida a un campo gravitatorio, o estar en el extremo de un muelle estirado,… posee una cierta energía potencial. Cuando el peso o la fuerza recuperadora actúan sobre la partícula, realizando trabajo sobre ella, lo hacen a costa de su energía potencial, que se ve reducida. | ||
| + | |||
| + | Podemos entender entonces que las partículas, por ocupar las posiciones que ocupan, almacenan una energía potencial, que se “gasta” en forma de trabajo sobre la partícula. | ||
| + | |||
| + | Asimismo, el signo negativo implica que la fuerza apunta en el sentido en que disminuye la energía potencial, es decir, la partícula tiende a acelerarse hacia donde su energía potencial es mínima. | ||
| + | |||
| + | En forma diferencial, la relación entre trabajo y energía potencial nos dice que lo que disminuye la energía potencial por unidad de tiempo es igual a la potencia desarrollada por las fuerzas conservativas | ||
| + | |||
| + | <center><math>-\mathrm{d}U = \delta{}W=\vec{F}_\mathrm{c}\cdot\mathrm{d}\vec{r}\qquad\Rightarrow\qquad -\frac{\mathrm{d}U}{\mathrm{d}t} =\vec{F}_\mathrm{c}\cdot\vec{v}=-P_\mathrm{c}</math></center> | ||
| + | |||
| + | ==Balance de energía== | ||
| + | Sobre una partícula actuarán, en general, tres tipos de fuerzas | ||
| + | * Fuerzas conservativas, <math>\vec{F}_c</math>, como el peso o la fuerza elástica | ||
| + | * Fuerzas que no realizan trabajo por ser normales a la velocidad, <math>\vec{F}_n</math>, como las reacciones asociadas a vínculos lisos (tensión, reacción de una superficie) | ||
| + | * Fuerzas no conservativas, <math>\vec{F}_{nc}</math>, como el rozamiento o como la fuerza que ejerce un agente externo como un motor. | ||
| + | Por ello, el trabajo total realizado sobre la partícula en su desplazamiento de un punto A a un punto B se compone de tres términos | ||
| + | <center><math>W^{A\to B}=\int_A^B\vec{F}_c\cdot\mathrm{d}\vec{r}+\int_A^B\vec{F}_n\cdot\mathrm{d}\vec{r}+\int_{\!\!\!\!\!\!\!\!C\ A}^B\vec{F}_c\cdot\mathrm{d}\vec{r}=-\Delta U+0+W^{A \to B}_{nc}</math></center> | ||
| + | Aquí la energía potencial es la suma de las correspondientes a cada una de las fuerzas conservativas que actúan sobre la partícula. | ||
| + | Por el teorema trabajo-energía cinética, esta cantidad es igual al incremento se su energía cinética | ||
| + | <center><math>\Delta K=-\Delta U+W_{nc}^{A\to B}</math></center> | ||
| + | Es decir, lo que aumenta la cinética es igual a lo que disminuye la potencial más el trabajo de las fuerzas no conservativas. Dado que este último es en muchos casos una cantidad negativa (disipación por rozamiento), podemos escribir este balance energético en la forma | ||
| + | <center><math>-\Delta U=\Delta K-W_{nc}^{A\to B}</math></center> | ||
| + | es decir, que la disminución de energía potencial se emplea en parte en incrementar la energía cinética y en parte se disipa por rozamiento. | ||
| + | Este balance tiene tres casos particulares de interés, cuando se anula cada uno de los tres términos: | ||
| + | *Si <math>\Delta U=0</math>, queda | ||
| + | <center><math>-\Delta K=-W_{nc}^{A\to B}</math></center> | ||
| + | :es decir, la energía cinética disminuye por la acción de fuerzas no conservativas como el rozamiento (también puede haber fuerzas no conservativas, como las ejercidas por un motor, que hacen aumentar la energía cinética). | ||
| + | *Si <math>\Delta K=0</math>, queda | ||
| + | <center><math>\Delta U=W_{nc}^{A\to B}</math></center> | ||
| + | :que leemos como que la energía potencial puede aumentar por la acción de fuerzas no conservativas. Así, una bomba de agua que eleva ésta a lo alto de una azotea, está aumentando la energía potencial gravitatoria. | ||
| + | *Si <math>W_{nc}^{A\to B}=0</math>, queda | ||
| + | <center><math>-\Delta U=\Delta K\,</math></center> | ||
| + | :que nos dice que en ausencia de fuerzas no conservativas, lo que aumenta la energía cinética es igual a lo que disminuye la potencial. Este es el caso en el que se conserva la energía mecánica, como veremos. | ||
| + | En forma diferencial, el balance de energía queda en la forma | ||
| + | <center><math>\frac{\mathrm{d}K}{\mathrm{d}t}=\vec{F}_c\cdot\vec{v}+\vec{F}_n\cdot\vec{v}+\vec{F}_{nc}\cdot\vec{v} ⃗=P_c+0+P_{nc}=-\frac{\mathrm{d}U}{\mathrm{d}t}+P_nc</math></center> | ||
| + | |||
| + | ==Energía mecánica== | ||
| + | Cuando una partícula está sometida exclusivamente a fuerzas conservativas, <math>\vec{F}_c</math> (como el peso) y a fuerzas que no realizan trabajo (como la tensión de un péndulo, <math>\vec{F}_T</math>), podemos calcular el trabajo realizado sobre la partícula como | ||
| + | |||
| + | <center><math>W_{A\to B} = \int_A^B \vec{F}_c\cdot\mathrm{d}\vec{r}+\overbrace{\int_A^B \vec{F}_T\cdot\mathrm{d}\vec{r}}^{=0}= U(A)-U(B) = -\Delta U</math></center> | ||
| + | |||
| + | esto es, el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial, calculada como la suma de las energías potenciales individuales (la debida al peso, más la elástica, más la eléctrica, etc.) | ||
| + | |||
| + | Combinando este teorema con el de las fuerzas vivas obtenemos | ||
| + | |||
| + | <center><math>-\Delta U = U(A) - U(B) = W_{A\to B} = K(B) - K(A) = \Delta K\,</math></center> | ||
| + | |||
| + | esto es, la que disminuye la energía potencial es igual a lo que aumenta la energía cinética (o viceversa). Reagrupando términos y definiendo la ''energía mecánica'' de la partícula como la suma de su energía cinética más la potencial obtenemos | ||
| + | |||
| + | <center><math>E(A) = K(A) + U(A) = K(B) + U(B) = E(B) = \mathrm{cte}\,</math></center> | ||
| + | |||
| + | lo que se conoce como ''teorema de conservación de la energía mecánica'': | ||
| + | |||
| + | :“''En ausencia de fuerzas no conservativas, la energía mecánica de una partícula permanece constante.''” | ||
| + | |||
| + | Si en vez de un proceso finito consideramos uno diferencial, el resultado es equivalente, | ||
| + | |||
| + | <center><math>-\mathrm{d}U = \delta W = \mathrm{d}K \qquad\Rightarrow\qquad \mathrm{d}U+\mathrm{d}K = 0</math></center> | ||
| + | |||
| + | Dividiendo por el tiempo empleado en realizar el proceso diferencial | ||
| + | |||
| + | <center><math>0=\frac{\mathrm{d}U}{\mathrm{d}t}+\frac{\mathrm{d}K}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}(U+K)= \frac{\mathrm{d}E}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | Este teorema deja de cumplirse cuando sobre la partícula actúan fuerzas no conservativas, como el rozamiento. Las fuerzas que reducen la energía mecánica (normalmente transformándola en calor) se conocen como ''fuerzas disipativas''. | ||
| + | |||
| + | Si sobre una partícula actúan tanto fuerzas conservativas como no conservativas, las consideramos por separado. Aplicando el teorema de las fuerzas vivas | ||
| + | |||
| + | <center><math>\Delta K = W_\mathrm{c}+W_\mathrm{nc}\,</math></center> | ||
| + | |||
| + | El trabajo de las fuerzas conservativas es igual a la disminución de su energía potencial | ||
| + | |||
| + | <center><math>\Delta K = -\Delta U + W_\mathrm{nc}\,</math></center> | ||
| + | |||
| + | Agrupando términos resulta que el incremento de la energía mecánica es igual al trabajo de las fuerzas no conservativas | ||
| + | |||
| + | <center><math>\Delta E = W_\mathrm{nc}\,</math></center> | ||
| + | |||
| + | En el caso particular de una fuerza de rozamiento, este trabajo es negativo y la energía mecánica disminuye como consecuencia de la fricción. | ||
| + | |||
| + | Si en lugar de considerar un incremento finito, calculamos la derivada respecto al tiempo obtenemos, por el teorema de las fuerzas vivas | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}K}{\mathrm{d}t}=P=P_\mathrm{c}+P_\mathrm{nc}=\vec{F}_\mathrm{c}\cdot\vec{v}+\vec{F}_\mathrm{nc}\cdot\vec{v}</math></center> | ||
| + | |||
| + | y por la potencia de las fuerzas conservativas | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}U}{\mathrm{d}t}=-P_\mathrm{c}=-\vec{F}_\mathrm{c}\cdot\vec{v}</math></center> | ||
| + | |||
| + | Sumando las dos | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}E}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}(K+U)=P_\mathrm{nc}=\vec{F}_\mathrm{nc}\cdot\vec{v}</math></center> | ||
| + | |||
| + | esto es, la derivada de la energía mecánica es la potencia desarrollada por las fuerzas no conservativas. | ||
| + | |||
| + | En particular, si la fuerza no conservativa es una de rozamiento dinámico, opuesta a la velocidad, resulta | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}E}{\mathrm{d}t}=\vec{F}_{r}\cdot\vec{v} < 0</math></center> | ||
| + | |||
| + | Dado que en todo sistema real siempre existen fuerzas de rozamiento, la conclusión es que en un sistema real sometido a fuerzas conservativas (que no modifican la energía mecánica) y disipativas (que la reducen) se tiende a la situación de mínima energía mecánica. | ||
| + | |||
| + | ===Ejemplos=== | ||
| + | El uso de razonamientos basados en la energía permite simplificar numerosos cálculos al prescindir del carácter vectorial de las magnitudes y poder omitir las fuerzas de reacción vincular que no realizan trabajo. | ||
| + | |||
| + | Entre los ejemplos inmediatos de aplicación están: | ||
| + | |||
| + | * La velocidad de impacto en la [[caída libre de un cuerpo (GIE)|caída libre de un cuerpo]] o de un [[Partícula en el interior de un aro|cuerpo sometido a vínculos lisos]]. | ||
| + | * La velocidad de oscilación de un [[Tensión de un péndulo|péndulo]] | ||
| + | * El intercambio entre energía cinética y potencial en un [[oscilador armónico]]. | ||
| + | * La [[Cálculo_de_energías_potenciales#Velocidad_de_escape|velocidad de escape]] de un campo gravitatorio. | ||
| + | |||
| + | ==Curvas de potencial== | ||
| + | [[Archivo:curva-energia-potencial.png|right]] | ||
| + | |||
| + | El análisis de la energía mecánica es especialmente útil en el caso de movimientos unidimensionales. Si tenemos una partícula cuyo movimiento se produce a lo largo de un eje OX, sometida a una fuerza dependiente sólo de la coordenada <math>x</math> | ||
| + | |||
| + | <center><math>\vec{r}(t) = x(t)\vec{\imath}</math>{{qquad}}{{qquad}}<math>\vec{F}=F(x)\vec{\imath}</math></center> | ||
| + | |||
| + | Para una fuerza de este tipo siempre existe una energía potencial dada por su integral respecto a <math>x</math> | ||
| + | |||
| + | <center><math>U(x) = -\int_{x_0}^x F(x)\,\mathrm{d}x</math>{{qquad}}{{qquad}}<math>F(x) = -\frac{\mathrm{d}U}{\mathrm{d}x}</math></center> | ||
| + | |||
| + | de forma que la ley de conservación de la energía mecánica se escribe | ||
| + | |||
| + | <center><math>\frac{1}{2}mv^2 + U(x) = E=\mathrm{cte}</math></center> | ||
| + | |||
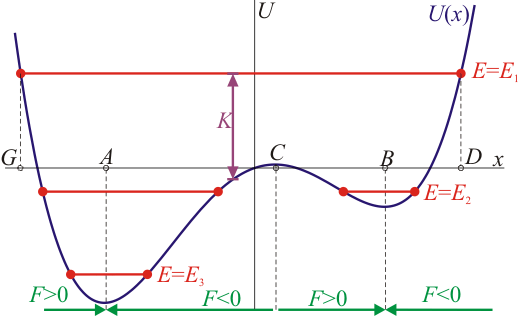
| + | Si trazamos la gráfica de la energía potencial <math>U=U(x)</math> como función de la posición <math>x</math>, podemos establecer varias propiedades del movimiento, que ilustraremos con el ejemplo de la figura. | ||
| + | |||
| + | * En primer lugar, es importante tener claro que esta gráfica ''no'' representa una curva bidimensional. No es una especie de montaña rusa en la que una bolita suba o baje, aunque comparta varias propiedades con este tipo de superficie. En la curva de potencial, la única coordenada es <math>x</math>. El eje de ordenadas representa la energía, no una distancia vertical. | ||
| + | * La curva de potencial permite establecer los puntos de equilibrio, así como la estabilidad de estos. | ||
| + | **Los puntos de equilibrio son aquellos para los que la fuerza sobre la partícula se anula. Esto corresponde a los extremos (máximos o mínimos) de la función <math>U(x)</math>. En el ejemplo serían las posiciones A, B y C. | ||
| + | **Dado que la fuerza sobre la partícula es la pendiente de la curva cambiada de signo, un mínimo de la energía potencial es un punto de equilibrio estable (A y B en el ejemplo), mientras que un máximo es un punto de equilibrio inestable (C en la figura). | ||
| + | * Un valor de la energía mecánica constante puede representarse como una recta horizontal en la gráfica (<math>E=E_1</math>, por ejemplo). En ese caso la diferencia entre esta recta y el valor de la curva en el mismo punto nos da el valor de la energía cinética, <math>K</math>. | ||
| + | * Puesto que la energía cinética no puede tener un valor negativo, el movimiento está acotado entre los puntos donde la recta de la energía mecánica corta a la curva de energía potencial. | ||
| + | * Los puntos donde la recta corta a la curva (D y G en la figura) son de energía cinética nula. En ellos la partícula queda en una posición de reposo instantáneo y la velocidad cambia de signo. Se denominan ''puntos de retorno''. | ||
| + | * Para un valor dado de la energía mecánica, puede existir varios estados de movimiento posibles. Así, para <math>E=E_2</math> la partícula puede oscilar en torno al punto A o en torno al punto B, pero no las dos cosas a la vez. Le es imposible atravesar la barrera de potencial situada en el máximo en C. | ||
| + | |||
| + | Como ilustración de casos sencillo, las siguientes son las curvas de potencial correspondientes a una pelota que se mueve verticalmente, sometida a la acción del peso y cuyo movimiento está limitado por el suelo, y el caso de un oscilador armónico, que describe un movimiento armónico simple. | ||
| + | |||
| + | <center> | ||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:curva-potencial-peso.png]] | ||
| + | | [[Archivo:curva-potencial-oscilador.png]] | ||
| + | | [[Archivo:curva-potencial-oscilador-rozamiento.png]] | ||
| + | |- | ||
| + | ! Caída libre | ||
| + | ! Oscilador armónico | ||
| + | ! Oscilador armónico con rozamiento | ||
| + | |- | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | En el caso de que haya fuerzas de fricción no conservativas la energía mecánica disminuye progresivamente y la partícula termina parándose en un punto de equilibrio estable. | ||
| + | |||
| + | ===Estabilidad de una partícula=== | ||
| + | El uso de la energía potencial y sus diagramas es el estudio de la estabilidad de una posición de equilibrio. Según se ve al estudiar las leyes de Newton, las posiciones de equilibrio pueden clasificarse en estables o inestables (hay más casos, cuando se considera la dependencia respecto a varias variables, pero aquí, por simplicidad, consideraremos solo una variable). | ||
| + | |||
| + | Consideremos, por ejemplo, un péndulo simple formado por una masa que cuelga de un punto de anclaje sujeto por una barra rígida sin masa. Este sistema posee dos posiciones de equilibrio: que la masa está en el punto más bajo del péndulo, o que esté en el punto más alto. Es claro que las dos posiciones no son equivalentes. Mientras que en la posición inferior la masa tiende a permanecer en ella, si se encuentra en el extremo superior cualquier pequeña perturbación hace que la masa caiga. | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:pendulo-estable.png]] | ||
| + | | [[Archivo:pendulo-inestable.png]] | ||
| + | |- | ||
| + | ! Estable | ||
| + | ! Inestable | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | Los puntos de equilibrio se clasifican en: | ||
| + | |||
| + | ;Estables: Ante una pequeña perturbación, tienden a retornar a la posición de equilibrio. El ejemplo representativo lo supone una partícula que rueda dentro de un cuenco, o una masa sujeta a un resorte. | ||
| + | |||
| + | ;Inestables: Una pequeña perturbación separa a la masa del equilibrio, y ésta tiende a alejarse de esta posición. Es el caso de una masa situada en lo alto de una cima o del péndulo invertido. También es el caso de una [[partícula en el interior de un tubo]] en rotación. Cuando se separa del centro, la inexistencia de una fuerza centrípeta hace que se aleje aun más. | ||
| + | |||
| + | ;Indiferente: La partícula no tiende a retornar a la posición de equilibrio, pero tampoco a alejarse de ella. Es el caso de una bola situada sobre una mesa horizontal. | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Archivo:equilibrio-estable.png]] | ||
| + | | [[Archivo:equilibrio-inestable.png]] | ||
| + | | [[Archivo:equilibrio-indiferente.png]] | ||
| + | |- | ||
| + | ! Estable | ||
| + | ! Inestable | ||
| + | ! Indiferente | ||
| + | |} | ||
| + | |||
| + | La clasificación se complica en 3 dimensiones por el hecho de que una posición de equilibrio puede ser estable respecto a fuerzas aplicadas en una dirección e inestable frente a otras aplicadas en una diferente. | ||
| + | |||
| + | También puede ocurrir que una misma posición de equilibrio pueda ser estable para ciertos valores de los parámetros (por ejemplo, la masa de la partícula) e inestable para valores diferentes. | ||
| + | |||
| + | En términos de la energía potencial, se trata de ver: | ||
| + | |||
| + | * Si <math>U</math> tiene un mínimo es una posición de equilibrio estable. | ||
| + | * Si <math>U</math> tiene un máximo es una posición de equilibrio inestable. | ||
| + | |||
| + | Cuando la energía es una función derivable se puede emplear el criterio de la segunda derivada: si es positiva se trata de un mínimo (equilibrio estable) y si es negativa se trata de un máximo (equilibrio inestable). | ||
| + | |||
| + | En el caso del equilibrio estable sin rozamiento, una partícula que esté cerca de la poisición de equilibrio oscilará alrededor de esta. Podemos calcular la frecuencia de estas oscilaciones con ayuda de la serie de Taylor | ||
| + | |||
| + | <center><math>U(x)\simeq U(x_0) + (x-x_0)\overbrace{\left.\frac{\mathrm{d}U}{\mathrm{d}x}\right|_{x_0}}^{=0}+\frac{1}{2}(x-x_0)^2\left.\frac{\mathrm{d}^2U}{\mathrm{d}x^2}\right|_{x_0}</math></center> | ||
| + | |||
| + | La primera derivada se anula porque la fuerza es nula en la posición de equilibrio. De forma más corta queda | ||
| + | |||
| + | <center><math>U(x)\simeq U_0+\frac{1}{2}k(x-x_0)^2 \qquad\qquad k = \left.\frac{\mathrm{d}^2U}{\mathrm{d}x^2}\right|_{x_0}</math></center> | ||
| + | |||
| + | Esta es la energía de un oscilador armónico de frecuencia | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{k}{m}}=\sqrt{\frac{1}{m}\left.\frac{\mathrm{d}^2U}{\mathrm{d}x^2}\right|_{x_0}}</math></center> | ||
| + | |||
| + | Más en general, si la posición se determina por una variable <math>\theta</math> tal que la energía cinética se puede escribir | ||
| + | |||
| + | <center><math>K = \frac{1}{2}A\dot{\theta}^2</math></center> | ||
| + | |||
| + | la frecuencia de las oscilaciones es | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{k}{A}}=\sqrt{\frac{1}{A}\left.\frac{\mathrm{d}^2U}{\mathrm{d}x^2}\right|_{x_0}}</math></center> | ||
| + | |||
| + | Así, para el péndulo simple tenemos | ||
| + | |||
| + | <center><math>K = \frac{1}{2}m|\vec{v}|^2 = \frac{1}{2}ml^2\dot{\varphi}^2 \qquad\Rightarrow\qquad A = m l^2</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>U(\varphi) = mgh = mgl(1-\cos(\varphi))\simeq \frac{mgl\varphi^2}{2}\qquad\Rightarrow\qquad k = mgl\,</math></center> | ||
| + | |||
| + | resultando la frecuencia | ||
| + | |||
| + | <center><math>\omega = \sqrt{\frac{mgl}{ml^2}}=\sqrt{\frac{g}{l}}</math></center> | ||
Revisión de 14:41 27 sep 2016
Contenido
|
1 Integrales primeras
Una constante de movimiento (también llamada integral primera) es una magnitud función de la posición, velocidad de la partícula (o de las partículas, si hay más de una) cuyo valor es constante, pese a que la posición y la velocidad sí son variables en el tiempo
Por ejemplo, supongamos una partícula que describe el movimiento circular
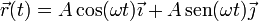
Este movimiento verifica las relaciones
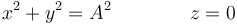
Así, aunque tanto x como y son funciones del tiempo, una combinación de las dos coordenadas permanece constante. Si hubiéramos conocido esta constancia antes de determinar la ley horaria, sabríamos que la trayectoria es una circunferencia, aunque la rapidez pudiera ser desconocida.
El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posición y velocidad en cualquier instante)
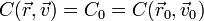
El ejemplo más conocido de constante de movimiento, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.
Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. A continuación estudiaremos tres magnitudes, construidas a partir de la posición y la velocidad, cuyas leyes de evolución pueden determinarse a partir de las leyes de Newton. Estas cantidades, si se dan las condiciones adecuadas, son candidatas a ser constantes de movimiento, y por tanto son las primeras candidatas cuando en un problema se buscan integrales primeras. Estas magnitudes son:
- La cantidad de movimiento
- El momento cinético o momento angular
- La energía mecánica
2 Cantidad de movimiento
2.1 Definición
Se define la cantidad de movimiento de una partícula como el producto de su masa por su velocidad
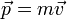
Sus dimensiones son MLT − 1 y sus unidades en el SI son  (o
(o 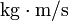 )
)
2.2 Teorema de la cantidad de movimiento
A partir de la definición es inmediato que

esto es, la derivada respecto al tiempo de la cantidad de movimiento es igual a la resultante de las fuerzas aplicadas sobre la partícula.
2.3 Impulso
En ocasiones, no nos interesa tanto saber cómo cambia la cantidad de movimiento en un intervalo de tiempo infinitesimal, sino saber cuánto varía durante un cierto periodo. Supongamos una partícula que viaja libremente y por tanto con cantidad de movimiento constante 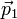 . Entonces es sometida a una fuerza
. Entonces es sometida a una fuerza 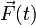 durante un intervalo entre t1 y t2 (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante
durante un intervalo entre t1 y t2 (por ejemplo, durante una colisión), a partir del cual vuelve a moverse libremente, con cantidad de movimiento constante 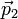 . Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. Integrando en la segunda ley de Newton obtenemos
. Se trata de hallar el incremento en la cantidad de movimiento durante la colisión. Integrando en la segunda ley de Newton obtenemos
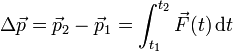
Esta integral de la fuerza sobre un intervalo recibe el nombre de impulso, por lo que la igualdad anterior establece que
- “El incremento de la cantidad de movimiento es igual al impulso recibido”
Esta relación, aparentemente trivial, tiene su importancia en la teoría de colisiones y de percusiones, donde se ignora el valor exacto de la fuerza, pero sí se conoce el valor del impulso.
Así, por ejemplo, en un saque de tenis, la rapidez de la pelota pasa de ser prácticamente nula a valer unos 60 m/s. Dado que la masa de una pelota es de 68 g, esto supone un impulso
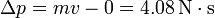
No conocemos la fuerza instantánea sobre la pelota, puesto que su deformación la convierte en un problema muy complejo. Podemos hallar la fuerza media, si conocemos el tiempo de colisión. Un valor típico podrían ser 30 ms, lo que nos da una fuerza media
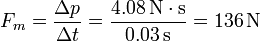
Por comparación, esta fuerza es 2000 veces el peso, o lo que es lo mismo, la pelota experimenta una aceleración de unos 200g.
2.4 Colisión con una pared
Un ejemplo de impulso lo tenemos en una colisión elástica con una pared. En este caso, la fuerza actúa sobre un tiempo muy corto ε, pero es capaz de producir un impulso
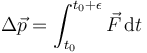
Carecemos de una expresión para la fuerza (aunque se puede modelar como una fuerza elástica). Podemos determinar el impulso a partir de su efecto.
2.4.1 Pared estacionaria
Si tenemos una partícula de masa m que impacta frontalmente con una superficie inmóvil se produce un cambio en la velocidad de la partícula, de forma que
- La componente tangente a la superficie no cambia
- La componente normal cambia de signo.
Supongamos que la superficie es el plano z = 0. En ese caso, si la velocidad inicial es
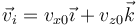
la velocidad tras la colisión será
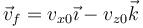
siendo el impulso sobre la partícula
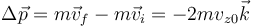
Colisiones como esta explican el concepto de presión a nivel microscópico. Cada una de las partículas de un gas que choca contra las paredes de un recipiente transfiere una cierta cantidad de movimiento. El conjunto de todas las colisiones por unidad de tiempo es una fuerza media. La fuerza por unidad de superficie es la presión.
2.4.2 Pared en movimiento
Si la pared está en movimiento (caso de una raqueta que golpea una pelota), el cambio de signo se da en la velocidad relativa, no en la absoluta.
En el caso unidimensional, si la velocidad inicial de la partícula y de la pared valen

la velocidad de la partícula relativa a la pared, antes de la colisión, es
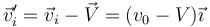
Tras la colisión, esta velocidad relativa invierte su sentido
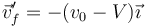
por lo que la nueva velocidad absoluta es
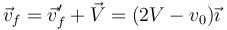
Vemos que tras la colisión, la partícula puede moverse más o menos rápido que antes, dependiendo de ambas velocidades. En particular, si la velocidad inicial es nula, sale disparada con una velocidad doble de la raqueta, y si la velocidad inicial es el doble de la de la raqueta, tras la colisión se queda clavada en el sitio.
El impulso en esta colisión es igual a

2.5 Teorema de conservación
De la segunda ley de Newton es inmediato que:
- “La cantidad de movimiento de una partícula permanece constante cuando la resultante de las fuerzas que actúan sobre ella es nula durante un intervalo de tiempo”
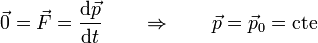
Puesto que la masa de la partícula permanece constante, si la cantidad de movimiento se conserva, la velocidad también permanece constante
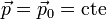

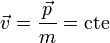
Por tanto, si la resultante de las fuerzas que actúan sobre la partícula se anula durante un intervalo de tiempo, la partícula se mueve uniformemente durante dicho periodo.
Esto no es exactamente lo mismo que lo que dice la Primera Ley de Newton, pues esta ley habla de partícula no sometida a ninguna interacción, mientras que el teorema de conservación se refiere a una partícula sometida a diferentes fuerzas, pero tales que su resultante es nula.
Para el caso de una partícula este teorema de conservación aporta poca información nueva. Sin embargo, su extensión al caso de un sistema de partículas es extremadamente útil.
3 Momento cinético
3.1 Definiciones
3.1.1 Momento cinético
Se define el momento cinético (o momento angular) de una partícula respecto a un punto fijo O como

siendo
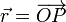
el vector de posición del punto P relativa al punto O.
3.1.2 Momento de una fuerza
Se define el momento respecto a un punto fijo O de una fuerza aplicada en un punto P como el producto vectorial
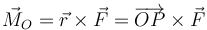
Al momento de una fuerza también se lo denomina “el par de la fuerza” o (por contagio del inglés) el “torque”.
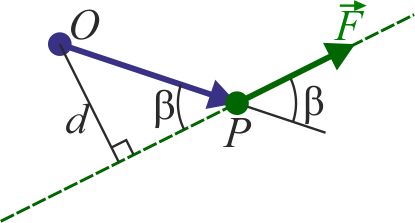
El módulo del momento de una fuerza es igual a
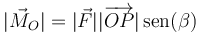
pero
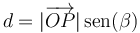
es la distancia a la llamada recta soporte, que es aquella que pasa por P y tiene la dirección de la fuerza. Por tanto, el módulo del momento de la fuerza se puede escribir
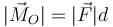
A la distancia d se la denomina “brazo del momento” o “brazo del par”. De aquí resulta que el valor del momento de una fuerza no depende de la posición exacta del punto P, sino solo de la recta soporte donde se halla.
La dirección del momento de la fuerza es perpendicular al plano definido por  y la fuerza (es decir, el que contiene a O y a la recta soporte). Su sentido lo da la regla de la mano derecha. Si O está a un lado de la recta soporte, el sentido del momento es hacia afuera del plano; si está al otro es hacia adentro. Cuando el propio punto O se encuentra en la recta soporte
y la fuerza (es decir, el que contiene a O y a la recta soporte). Su sentido lo da la regla de la mano derecha. Si O está a un lado de la recta soporte, el sentido del momento es hacia afuera del plano; si está al otro es hacia adentro. Cuando el propio punto O se encuentra en la recta soporte
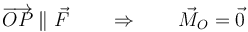
Si tenemos varias fuerzas actuando sobre la misma partícula, la resultante de los momentos es igual al momento de la resultante
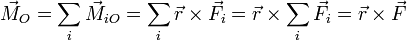
3.2 Interpretación del momento cinético
Del mismo modo que la cantidad de movimiento, como su nombre indica, es una medida de cuánto se mueve una partícula (en el sentido de que, por ejemplo, en una colisión, importa tanto la velocidad del proyectil como su masa), el momento cinético mide la cantidad de rotación en torno al punto O.
Esto se ve claro en el caso de un movimiento circular. Si una partícula describe una circunferencia alrededor del punto O, el momento cinético respecto a este punto vale

Vemos que esta “cantidad de rotación” depende de con qué velocidad se gira, de la masa de la partícula y del radio de la circunferencia.
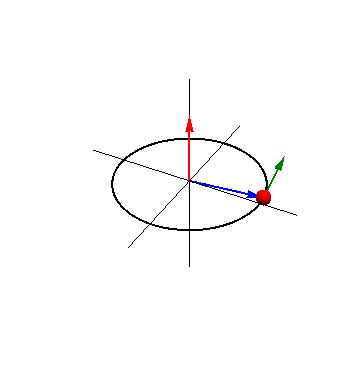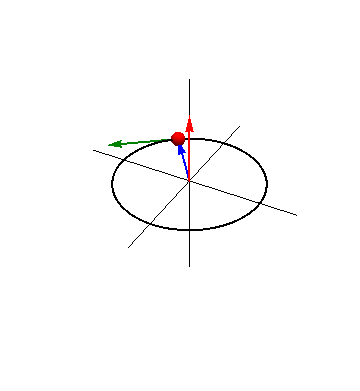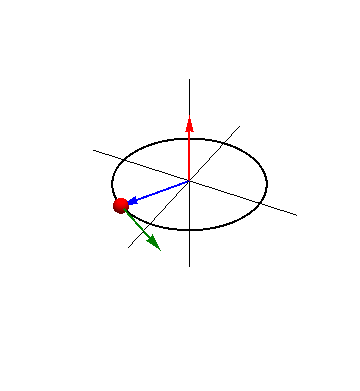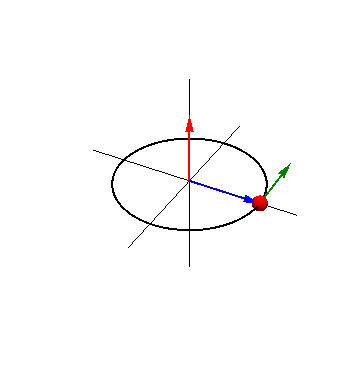
Esta idea se puede generalizar a movimientos no circulares. Si una partícula describe un movimiento rectilíneo y la observamos desde un punto exterior a la recta, nuestra dirección de observación va girando, aunque la partícula vaya en línea recta. Eso sí, cuanto mayor es la distancia, menor es el cambio de la dirección de observación.
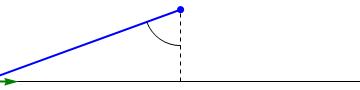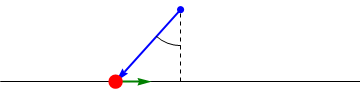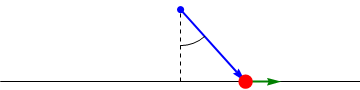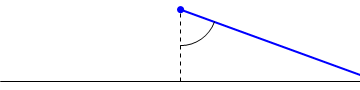
3.3 Cambio del centro de reducción
Si en vez de un punto O, calculamos el momento cinético respecto a otro punto fijo A
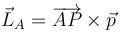
la relación con el del punto O es
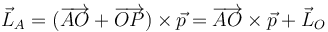
siendo el vector  uno fijo, independiente del movimiento de la partícula. Invirtiendo el producto vectorial
uno fijo, independiente del movimiento de la partícula. Invirtiendo el producto vectorial
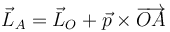
Igualmente, para el momento de las fuerzas, tenemos que
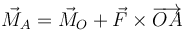
siendo  la resultante de las fuerzas aplicadas
la resultante de las fuerzas aplicadas
3.4 Derivada del momento cinético (Teorema del momento cinético)
Como consecuencia de la segunda ley de Newton, la derivada del momento cinético de una partícula es igual al momento resultante sobre ella

Para que esta expresión sea correcta, el punto O debe ser un punto fijo.
3.5 Teorema de conservación
De la expresión para la derivada del momento cinético se deduce su teorema de conservación:
- Si la resultante de los momentos de las fuerzas que actúan sobre una partícula es nula, el momento cinético de dicha partícula permanece constante.
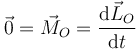

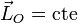
Una consecuencia inmediata de la conservación del momento cinético es:
- La trayectoria de una partícula cuyo momento cinético permanece constante es plana.
El plano en el que ocurre la trayectoria es el definido por el centro de reducción, la posición inicial y la velocidad inicial.
Puesto que el momento cinético se conserva tenemos que si multiplicamos escalarmente el vector de posición relativo por este vector constante
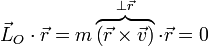
Esta es la ecuación vectorial de un plano que pasa por O y es normal a la dirección de  .
.
3.6 Fuerzas centrales
Las fuerzas centrales constituyen un caso particular e importante de las diferentes fuerzas presentes en la naturaleza. Una fuerza central es aquella que en todos los puntos del espacio posee dirección radial desde un punto fijo O, siendo además dependiente solo de la distancia a dicho punto
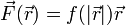
Ejemplos de fuerzas centrales son la fuerza de la gravedad debida a un objeto masivo (como la atracción que el Sol ejerce sobre la Tierra), o la fuerza eléctrica debida a una carga en reposo.
Se tiene que
- El momento cinético respecto a un punto O de una partícula sometida a la acción de una fuerza central, con centro O, permanece constante.
La demostración es inmediata, ya que el vector de posición relativo y la fuerza son vectores paralelos

En particular, esto implica que la trayectoria de toda partícula sometida a una fuerza central (p.ej. una óirbita planetaria, o un oscilador armónico en 3 dimensiones) es una curva plana.
3.7 Ejemplo. Péndulo simple
Un ejemplo de aplicación del teorema del momento cinético en el que se simplifican los cálculos respecto a la aplicación directa de las leyes de Newton es el caso del péndulo simple.
Supongamos una partícula de masa m atada a un hilo inextensible que por su otro extremo está atado a un punto de anclaje fijo O.
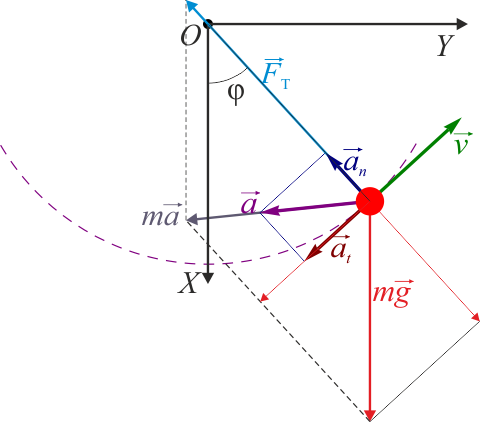
Tal como se ve en el apartado correspondiente de aplicaciones de las leyes de Newton, la masa se encuentra sometida a la acción conjunto de dos fuerzas: el peso y la tensión del hilo, de forma que
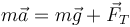
Desarrollando esta ecuación en sus componentes y eliminando la tensión entre las dos ecuaciones que resultan se llega a la ecuación del péndulo
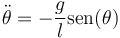
la complicación que tiene este método es que obliga a introducir la tensión, que es una fuerza desconocida a priori.
Veamos como sería con ayuda del momento cinético. El momento cinético respecto al punto O es igual a

donde

Al ser perpendiculares estos dos vectores, su producto vectorial es igual a
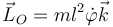
siendo  el vector normal hacia afuera del plano de oscilación del péndulo (no el de la dirección de la gravedad, que en estos ejes sería
el vector normal hacia afuera del plano de oscilación del péndulo (no el de la dirección de la gravedad, que en estos ejes sería 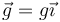 ). La derivada respecto al tiempo del momento cinético es
). La derivada respecto al tiempo del momento cinético es
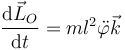
Esta derivada debe ser igual a la resultante de los momento de las fuerzas aplicadas
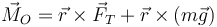
Ahora bien, la tensión va en la dirección del hilo, que es también la del vector de posición. Por tanto, su momento es nulo y solo queda el del peso. Éste, a su vez, es igual a la distancia a la recta soporte (la vertical que pasa por la partícula), con lo que su momento vale
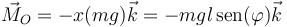
el signo negativo viene de que cuando  es positivo, la regla de la mano derecha da para el momento un sentido hacia adentro del plano.
es positivo, la regla de la mano derecha da para el momento un sentido hacia adentro del plano.
Igualando las dos cantidades queda
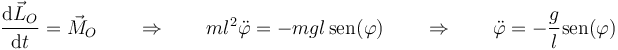
4 Trabajo y energía cinética
4.1 Trabajo de una fuerza constante
Cuando una fuerza constante se aplica sobre un cuerpo que realiza un desplazamiento Δx en la dirección de la fuerza aplicada, se dice que la fuerza realiza un trabajo
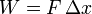
Vemos que las unidades en las que se mide el trabajo son las de una fuerza por una distancia, siendo la unidad SI 1 julio = 1 newton·m.
El trabajo es positivo si la fuerza se aplica en el mismo sentido que se realiza el desplazamiento y negativo si se opone a él. El trabajo es nulo si no hay desplazamiento. Una persona puede ejercer toda la fuerza que quiera contra una pared, hasta agotarse. Si la pared no se mueve, no ha realizado trabajo alguno.
Si la fuerza, como vector que es, posee una dirección diferente al desplazamiento, solo su componente en la dirección de este realiza trabajo

Esta cantidad de expresa de manera más sencilla con ayuda del producto escalar
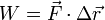
Vemos que
- El trabajo es una cantidad escalar, con signo.
- No se realiza trabajo si se ejerce una fuerza pero no se produce desplazamiento.
- Una fuerza perpendicular al desplazamiento no realiza trabajo alguno.
4.2 Trabajo de una fuerza variable
Si tenemos una partícula que realiza una trayectoria arbitraria, sometida a una fuerza variable con la posición o el tiempo, podemos hallar el trabajo dividiendo el camino en diferenciales casi rectilíneos, calculando el trabajo (diferencial) en cada uno, y sumando (integrando) el resultado.
El trabajo diferencial es igual a
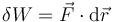
A partir de aquí obtenemos el trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C como la suma de los trabajos elementales a lo largo de dicha curva
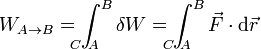
Respecto a la notación, el hecho de que el trabajo diferencial (que no diferencial de trabajo) se represente como δW en lugar de dW se debe justamente al hecho de que es una cantidad que depende del camino, como se estudia en más detalle en Termodinámica.
4.3 Trabajo de la superposición de varias fuerzas
Si sobre una partícula actúan varias fuerzas simultáneamente, por el principio de superposición, el trabajo total será igual a la suma de los trabajos individuales
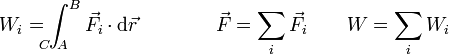
4.4 Potencia
A partir del trabajo, se define la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo dt, dividido por dicho intervalo

De esta definición resulta que la potencia tiene dimensiones de trabajo partido por tiempo (o fuerza multiplicada por velocidad), siendo su unidad el vatio (W), igual a un 1 J/s.
4.5 Energía cinética. Teorema de la fuerzas vivas
4.5.1 Caso de una fuerza constante
En el caso de una partícula sometida a una fuerza neta constante, el resultado es un movimiento con aceleración constante.
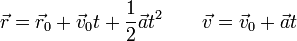
Si multiplicamos escalarmente la segunda ecuación por sí misma nos queda
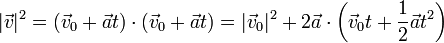
y teniendo en cuenta el desplazamiento dado por la ecuación horaria nos queda
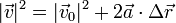
Multiplicando por la masa y dividiendo por 2 nos queda finalmente
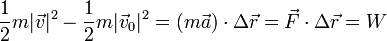
que podemos abreviar como
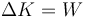
siendo K una cantidad que llamamos energía cinética de la partícula
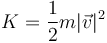
4.5.2 Caso de una fuerza variable
Si tenemos una trayectoria arbitraria que va del punto A al punto B y la partícula está sometida a una fuerza neta variable, simplemente dividimos el camino en pequeñas porciones en cada una de las cuales puede suponerse la fuerza prácticamente constante. Para cada uno de estos diferenciales de camino se cumplirá
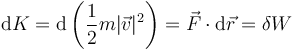
y sumando para todas las porciones obtenemos la relación
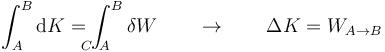
La identidad
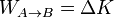
se conoce como teorema de las fuerzas vivas (o teorema trabajo-energía cinética).
4.5.3 Interpretación
El teorema de las fuerzas vivas

requiere una cierta interpretación ya que se presta a confusiones. Lo enunciamos primero con palabras:
- El trabajo realizado entre dos puntos por la resultante de las fuerzas que actúan sobre una partícula es igual al incremento de la energía cinética entre dichos dos puntos
Es decir, si se hace un trabajo positivo sobre la partícula, su energía cinética aumenta, esto es, se mueve más rápido. Si por contra el trabajo es negativo, oponiéndose al movimiento, la energía cinética disminuye y la partícula se mueve más despacio.
Si la partícula tiene en el punto B la misma rapidez que en el punto A, su energía cinética no ha cambiado y por tanto el trabajo neto realizado sobre ella es nulo, independientemente de que haya existido una fuerza actuando sobre ella, acelerándola en los puntos intermedios.
Hay que remarcar que el teorema de las fuerzas vivas habla de la fuerza neta, esto es, la resultante de las fuerzas aplicadas. Si sobre una partícula actúan varias fuerzas simultáneamente, cada una de ellas realizará un trabajo, pero cada uno de ellos no es igual a la variación de la energía cinética, solo su suma lo es.
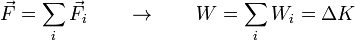
También hay que remarcar otro aspecto de la expresión del teorema. Puede aparecer extraño que de la relación
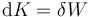
no se deduzca la igualdad entre dos incrementos. La razón es profunda y se relaciona con conceptos más generales que se estudian en Termodinámica. La idea es la siguiente:
- La energía cinética es una función de estado: esto quiere decir que conocido el estado de la partícula (su posición y su velocidad instantáneas), podemos hallar su energía cinética
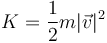
- y su valor es uno solo. Podemos imaginar que la partícula, por moverse con la rapidez que lo hace, almacena una cierta cantidad de energía cinética. Por ello, el incremento de K es igual a su valor en B menos su valor en A.
- El trabajo no es una función de estado, sino que depende del camino: no nos basta con saber qué posición y que velocidad tiene la partícula en un momento dado, sino que necesitamos saber qué curva ha descrito (por ello se indica una C en la integral correspondiente) y qué fuerza ha actuado sobre ella en cada punto del camino. El trabajo es por sí mismo una integral. No es el incremento ni la variación de nada. No podemos decir que la partícula almacena un trabajo.
Por ello, los dos diferenciales anteriores son de distinto tipo y se representan con letras diferentes, el de la energía con d y el del trabajo con δ. El diferencial de energía es un incremento muy pequeño de una función. El trabajo diferencial es una cantidad muy pequeña de trabajo realizado.
Así, el teorema de las fuerzas vivas representa que un trabajo realizado sobre una partícula se “almacena” en forma de energía cinética.
4.5.4 Forma diferencial del teorema
A partir de la relación entre los diferenciales podemos escribir el teorema de las fuerzas vivas como una relación entre derivadas en lugar de integrales.
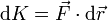
Dividiendo por el diferencial de tiempo empleado en realizar el desplazamiento
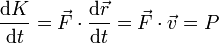
esto es, en cada instante, la derivada respecto al tiempo de la energía cinética es igual a la potencia neta realizada sobre la partícula.
4.5.5 Aplicación a colisiones
Cuando se produce una colisión, una partícula experimenta una fuerza muy intensa durante un periodo de tiempo muy corto. Esta fuerza es capaz de producir un cambio neto en la cantidad de movimiento (el impulso). También puede producir un incremento en la energía cinética
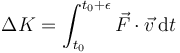
Así, en el caso de una colisión oblicua contra una pared estacionaria en z = 0 tenemos las velocidades antes y después del choque

y por tanto el incremento de la energía cinética en este caso es nulo
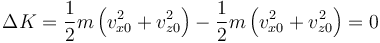
Por ello se dice que tenemos una colisión elástica.
En el caso de un choque frontal contra una pared en movimiento las velocidades inicial y final valen
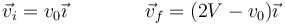
por lo que resulta un incremento de energía cinética que no será nulo en general

Se anulará si la pared está en reposo (caso anterior) o si la partícula se mueve con la misma velocidad que la pared (con lo que no llegan a chocar).
4.6 Teorema de conservación de la energía cinética
Este teorema implica, entre otras resultados, que
- “Una partícula sometida a una fuerza puramente normal a su trayectoria (o nula) en todo momento mantiene constante su energía cinética y por tanto se mueve de manera uniforme (aunque la dirección de movimiento sea cambiante).”
Ejemplo de fuerzas permanentemente normales a la trayectoria son:
- La fuerza magnética
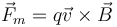
- La fuerza de Coriolis que aparece en sistemas no inerciales.
- Las fuerzas de reacción vincular debidas a vínculos sin rozamiento e independientes del tiempo.
Esta última propiedad es especialmente importante porque permite aplicar el teorema de conservación de la energía mecánica a partículas vinculadas, sin necesidad de considerar las fuerzas de reacción a la hora de calcular la energía. Por ejemplo, puede hallarse la velocidad de una masa que desciende por un plano inclinado empleando razonamientos energéticos sin incluir la reacción normal al plano.
4.7 Ejemplos
4.7.1 Trabajo debido al peso
El peso de un cuerpo es una fuerza constante, por lo que se aplica directamente el resultado anterior, sin necesidad de hacer integral alguna

Teniendo en cuenta la expresión del vector de posición en cartesianas
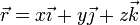
nos queda, para el trabajo
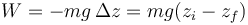
Este trabajo es igual al aumento de la energía cinética

Igualando ambas cantidades
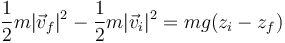
En el caso particular de un objeto que cae desde una altura h, partiendo del reposo, y llega hasta el suelo

Nos queda, para la rapidez de impacto

Obsérvese que el resultado es independiente de que el objeto caiga verticalmente o describiendo una parábola.
4.7.2 Trabajo de un oscilador armónico
El teorema de las fuerzas vivas posee numerosas aplicaciones, ya que permite determinar celeridades sin necesidad de resolver la ecuación de movimiento.
Consideremos el caso de un oscilador armónico que se libera desde el reposo a una distancia A del punto de equilibrio. ¿Que rapidez tiene la masa cuando pasa por éste? ¿Qué trabajo se realiza entre el punto inicial y el de máxima elongación al otro lado de la posición de equilibrio?
El trabajo que realiza la fuerza recuperadora entre la posición inicial y la de equilibrio vale
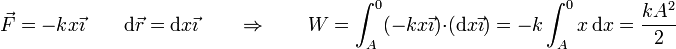
Este trabajo es igual al incremento de energía cinética

vemos que hallamos la rapidez en el punto de equilibrio sin necesidad de usar los senos y cosenos que nos dan las ecuaciones horarias.
Para la segunda cuestión, el trabajo realizado entre el punto inicial (de velocidad nula) y el punto opuesto de máxima elongación (que también es un punto de reposo instantáneo) es nulo.

4.7.3 Partícula que desliza por un aro
Sea una pequeña anilla de masa m ensartada en un aro circular de radio R puesto verticalmente. Si la anilla se suelta desde el reposo en el punto más alto del aro y el rozamiento es despreciable, ¿con qué velocidad llega al punto más bajo?
La partícula está sometida a dos fuerzas, su peso y la fuerza de reacción del aro.
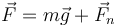
El trabajo total realizado sobre la partícula será la suma de los dos trabajos individuales

El trabajo de la fuerza de reacción es nulo, ya que la fuerza es perpendicular en todo momento al desplazamiento
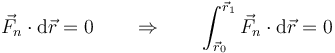
El trabajo debido al peso se halla, como antes, observando que se trata de una fuerza constante (o bien, explícitamente por la integral, como en un problema) y el resultado es
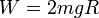
Esto nos da la rapidez final
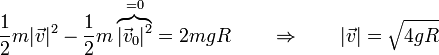
Obsérvese que aunque la fuerza de reacción no realice trabajo sí que acelera a la partícula, cambiando su dirección de movimiento. Si solo actuara el peso, la anilla caería verticalmente. Es la fuerza de reacción la que hace en el punto más bajo la velocidad sea horizontal.
4.7.4 Disipación de energía cinética
En el caso de una partícula sometida exclusivamente a una fuerza de rozamiento dinámico (seco o viscoso), la energía cinética disminuye de forma continuada, ya que
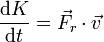
Dado que la fuerza de rozamiento dinámico se opone a la velocidad, este producto escalar es negativo y la energía cinética disminuye.
En particular, en el caso de un rozamiento viscoso lineal nos queda
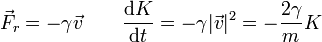
Separando diferenciales e integrando llegamos a un decaimiento exponencial en la energía cinética
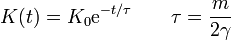
El tiempo que tarda la energía en disiparse es independiente de la velocidad inicial. Sí depende de la masa de la partícula. Cuanto mayor sea su masa, y por tanto su inercia, más lentamente decae la energía.
5 Energía potencial
5.1 Definición
El trabajo realizado por una fuerza cuando una partícula se mueve desde un punto A a un punto B depende en general del camino recorrido. Por ejemplo, una fuerza de rozamiento realiza un trabajo mayor cuanto mayor sea la distancia recorrida, aunque los puntos iniciales y finales sean los mismos en todos los caminos.
Existe una clase de fuerzas, denominadas fuerzas conservativas, para las cuales el trabajo entre dos puntos es independiente del camino que se emplea para ir de uno a otro
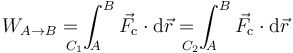
Esto permite definir una función denominada energía potencial como el trabajo, cambiado de signo, para ir desde un punto fijo O (el origen de potencial) hasta un punto fijo
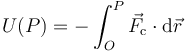
Entre los casos importantes de fuerzas conservativas tenemos:
- El peso, para el cual, si el origen de potencial es la superficie terrestre y z la altura sobre ella:
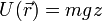
- Más en general la fuerza gravitatoria producida por un cuerpo fijo sobre otro, tomando como origen de potencial el infinito, tiene una energía potencial
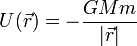
- El oscilador armónico, que cumple la ley de Hooke, tomando el origen de potencial en el punto de equilibrio, tiene una energía potencial, en el caso rectilíneo
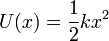
- y en el caso general
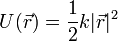
La energía potencial se obtiene a partir de la fuerza, integrando respecto a la posición. Para ello hay que elegir un camino (que es arbitrario, pero uno hay que elegir) que lleve del origen de potencial al punto donde queremos hallar el potencial.
En el caso de una fuerza dependiente de la posición a lo largo de una recta que actúa sobre una partícula que se mueve sobre esta recta, el camino es inmediato: es la propia recta de movimiento

y la integral de camino se reduce a una integral usual

Así, para el caso del oscilador armónico, tomando como origen de potencial la posición de equilibrio
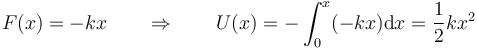
En tres dimensiones el problema es más complicado, aunque para fuerzas centrales podemos tomar un camino rectilíneo radial
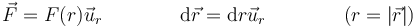
y para el oscilador armónico en tres dimensiones resulta
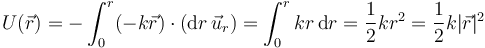
De manera similar se calcula la energía potencial gravitatoria.
Inversamente, se puede hallar la fuerza, conocida la energía potencial, derivando respecto a la posición.
En el caso de un movimiento rectilíneo la energía potencial depende solo de una variable, x, y la fuerza es igual a
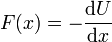
En el caso general del movimiento tridimensional, una fuerza conservativa se calcula a partir de la energía potencial hallando el gradiente:
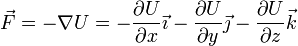
donde las derivadas son parciales, esto es, calculadas derivando respecto a una coordenada tratando al resto de coordenadas como constantes.
Por ejemplo, para la energía potencial de un oscilador armónico, en el caso rectilíneo

En tres dimensiones

hallando las tres derivadas parciales obtenemos la fuerza
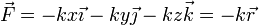
5.2 Trabajo y energía potencial
Con la definición de energía potencial se cumple, para fuerzas conservativas,

La demostración es la siguiente. Debemos hallar el trabajo en el camino de A a B. Si  es conservativa, podemos elegir el camino que queramos para ir de un punto a otro. Tomamos entonces una ruta que pasa por O.
es conservativa, podemos elegir el camino que queramos para ir de un punto a otro. Tomamos entonces una ruta que pasa por O.
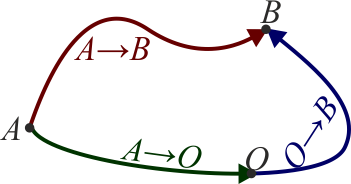
Entonces se cumple

La identidad anterior es similar al teorema de las fuerzas vivas, con dos diferencias importantes:
- Solo se aplica a fuerzas conservativas, no a todas las fuerzas (en particular, no al rozamiento).
- Nos habla de lo que ocurre de una fuerza individual. En una partícula sometida a varias fuerzas, cada una podrá o no derivar de una energía potencial. El teorema de las fuerzas vivas habla de la resultante de todas las fuerzas aplicadas.
- Hay un signo menos, con lo que el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial.
Podemos interpretar entonces el resultado diciendo que la partícula por estar sometida a un campo gravitatorio, o estar en el extremo de un muelle estirado,… posee una cierta energía potencial. Cuando el peso o la fuerza recuperadora actúan sobre la partícula, realizando trabajo sobre ella, lo hacen a costa de su energía potencial, que se ve reducida.
Podemos entender entonces que las partículas, por ocupar las posiciones que ocupan, almacenan una energía potencial, que se “gasta” en forma de trabajo sobre la partícula.
Asimismo, el signo negativo implica que la fuerza apunta en el sentido en que disminuye la energía potencial, es decir, la partícula tiende a acelerarse hacia donde su energía potencial es mínima.
En forma diferencial, la relación entre trabajo y energía potencial nos dice que lo que disminuye la energía potencial por unidad de tiempo es igual a la potencia desarrollada por las fuerzas conservativas

6 Balance de energía
Sobre una partícula actuarán, en general, tres tipos de fuerzas
- Fuerzas conservativas,
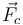 , como el peso o la fuerza elástica
, como el peso o la fuerza elástica
- Fuerzas que no realizan trabajo por ser normales a la velocidad,
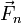 , como las reacciones asociadas a vínculos lisos (tensión, reacción de una superficie)
, como las reacciones asociadas a vínculos lisos (tensión, reacción de una superficie)
- Fuerzas no conservativas,
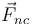 , como el rozamiento o como la fuerza que ejerce un agente externo como un motor.
, como el rozamiento o como la fuerza que ejerce un agente externo como un motor.
Por ello, el trabajo total realizado sobre la partícula en su desplazamiento de un punto A a un punto B se compone de tres términos
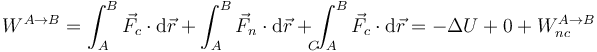
Aquí la energía potencial es la suma de las correspondientes a cada una de las fuerzas conservativas que actúan sobre la partícula. Por el teorema trabajo-energía cinética, esta cantidad es igual al incremento se su energía cinética
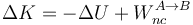
Es decir, lo que aumenta la cinética es igual a lo que disminuye la potencial más el trabajo de las fuerzas no conservativas. Dado que este último es en muchos casos una cantidad negativa (disipación por rozamiento), podemos escribir este balance energético en la forma
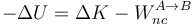
es decir, que la disminución de energía potencial se emplea en parte en incrementar la energía cinética y en parte se disipa por rozamiento. Este balance tiene tres casos particulares de interés, cuando se anula cada uno de los tres términos:
- Si ΔU = 0, queda
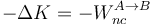
- es decir, la energía cinética disminuye por la acción de fuerzas no conservativas como el rozamiento (también puede haber fuerzas no conservativas, como las ejercidas por un motor, que hacen aumentar la energía cinética).
- Si ΔK = 0, queda

- que leemos como que la energía potencial puede aumentar por la acción de fuerzas no conservativas. Así, una bomba de agua que eleva ésta a lo alto de una azotea, está aumentando la energía potencial gravitatoria.
- Si
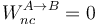 , queda
, queda
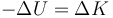
- que nos dice que en ausencia de fuerzas no conservativas, lo que aumenta la energía cinética es igual a lo que disminuye la potencial. Este es el caso en el que se conserva la energía mecánica, como veremos.
En forma diferencial, el balance de energía queda en la forma
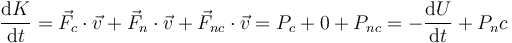
7 Energía mecánica
Cuando una partícula está sometida exclusivamente a fuerzas conservativas, 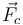 (como el peso) y a fuerzas que no realizan trabajo (como la tensión de un péndulo,
(como el peso) y a fuerzas que no realizan trabajo (como la tensión de un péndulo, 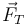 ), podemos calcular el trabajo realizado sobre la partícula como
), podemos calcular el trabajo realizado sobre la partícula como

esto es, el trabajo realizado sobre la partícula es igual a la disminución de su energía potencial, calculada como la suma de las energías potenciales individuales (la debida al peso, más la elástica, más la eléctrica, etc.)
Combinando este teorema con el de las fuerzas vivas obtenemos
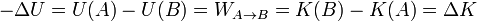
esto es, la que disminuye la energía potencial es igual a lo que aumenta la energía cinética (o viceversa). Reagrupando términos y definiendo la energía mecánica de la partícula como la suma de su energía cinética más la potencial obtenemos
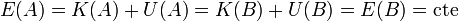
lo que se conoce como teorema de conservación de la energía mecánica:
- “En ausencia de fuerzas no conservativas, la energía mecánica de una partícula permanece constante.”
Si en vez de un proceso finito consideramos uno diferencial, el resultado es equivalente,

Dividiendo por el tiempo empleado en realizar el proceso diferencial
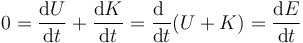
Este teorema deja de cumplirse cuando sobre la partícula actúan fuerzas no conservativas, como el rozamiento. Las fuerzas que reducen la energía mecánica (normalmente transformándola en calor) se conocen como fuerzas disipativas.
Si sobre una partícula actúan tanto fuerzas conservativas como no conservativas, las consideramos por separado. Aplicando el teorema de las fuerzas vivas
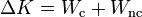
El trabajo de las fuerzas conservativas es igual a la disminución de su energía potencial
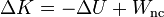
Agrupando términos resulta que el incremento de la energía mecánica es igual al trabajo de las fuerzas no conservativas
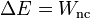
En el caso particular de una fuerza de rozamiento, este trabajo es negativo y la energía mecánica disminuye como consecuencia de la fricción.
Si en lugar de considerar un incremento finito, calculamos la derivada respecto al tiempo obtenemos, por el teorema de las fuerzas vivas
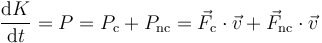
y por la potencia de las fuerzas conservativas
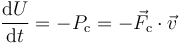
Sumando las dos

esto es, la derivada de la energía mecánica es la potencia desarrollada por las fuerzas no conservativas.
En particular, si la fuerza no conservativa es una de rozamiento dinámico, opuesta a la velocidad, resulta
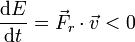
Dado que en todo sistema real siempre existen fuerzas de rozamiento, la conclusión es que en un sistema real sometido a fuerzas conservativas (que no modifican la energía mecánica) y disipativas (que la reducen) se tiende a la situación de mínima energía mecánica.
7.1 Ejemplos
El uso de razonamientos basados en la energía permite simplificar numerosos cálculos al prescindir del carácter vectorial de las magnitudes y poder omitir las fuerzas de reacción vincular que no realizan trabajo.
Entre los ejemplos inmediatos de aplicación están:
- La velocidad de impacto en la caída libre de un cuerpo o de un cuerpo sometido a vínculos lisos.
- La velocidad de oscilación de un péndulo
- El intercambio entre energía cinética y potencial en un oscilador armónico.
- La velocidad de escape de un campo gravitatorio.
8 Curvas de potencial
El análisis de la energía mecánica es especialmente útil en el caso de movimientos unidimensionales. Si tenemos una partícula cuyo movimiento se produce a lo largo de un eje OX, sometida a una fuerza dependiente sólo de la coordenada x
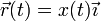
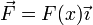
Para una fuerza de este tipo siempre existe una energía potencial dada por su integral respecto a x

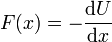
de forma que la ley de conservación de la energía mecánica se escribe
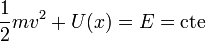
Si trazamos la gráfica de la energía potencial U = U(x) como función de la posición x, podemos establecer varias propiedades del movimiento, que ilustraremos con el ejemplo de la figura.
- En primer lugar, es importante tener claro que esta gráfica no representa una curva bidimensional. No es una especie de montaña rusa en la que una bolita suba o baje, aunque comparta varias propiedades con este tipo de superficie. En la curva de potencial, la única coordenada es x. El eje de ordenadas representa la energía, no una distancia vertical.
- La curva de potencial permite establecer los puntos de equilibrio, así como la estabilidad de estos.
- Los puntos de equilibrio son aquellos para los que la fuerza sobre la partícula se anula. Esto corresponde a los extremos (máximos o mínimos) de la función U(x). En el ejemplo serían las posiciones A, B y C.
- Dado que la fuerza sobre la partícula es la pendiente de la curva cambiada de signo, un mínimo de la energía potencial es un punto de equilibrio estable (A y B en el ejemplo), mientras que un máximo es un punto de equilibrio inestable (C en la figura).
- Un valor de la energía mecánica constante puede representarse como una recta horizontal en la gráfica (E = E1, por ejemplo). En ese caso la diferencia entre esta recta y el valor de la curva en el mismo punto nos da el valor de la energía cinética, K.
- Puesto que la energía cinética no puede tener un valor negativo, el movimiento está acotado entre los puntos donde la recta de la energía mecánica corta a la curva de energía potencial.
- Los puntos donde la recta corta a la curva (D y G en la figura) son de energía cinética nula. En ellos la partícula queda en una posición de reposo instantáneo y la velocidad cambia de signo. Se denominan puntos de retorno.
- Para un valor dado de la energía mecánica, puede existir varios estados de movimiento posibles. Así, para E = E2 la partícula puede oscilar en torno al punto A o en torno al punto B, pero no las dos cosas a la vez. Le es imposible atravesar la barrera de potencial situada en el máximo en C.
Como ilustración de casos sencillo, las siguientes son las curvas de potencial correspondientes a una pelota que se mueve verticalmente, sometida a la acción del peso y cuyo movimiento está limitado por el suelo, y el caso de un oscilador armónico, que describe un movimiento armónico simple.
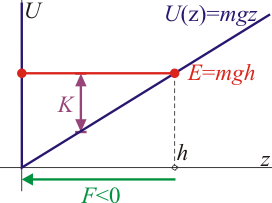
| 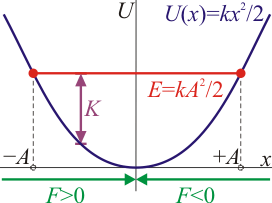
| 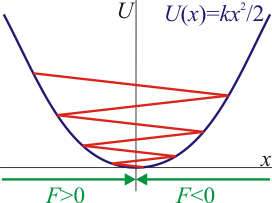
|
| Caída libre | Oscilador armónico | Oscilador armónico con rozamiento |
|---|
En el caso de que haya fuerzas de fricción no conservativas la energía mecánica disminuye progresivamente y la partícula termina parándose en un punto de equilibrio estable.
8.1 Estabilidad de una partícula
El uso de la energía potencial y sus diagramas es el estudio de la estabilidad de una posición de equilibrio. Según se ve al estudiar las leyes de Newton, las posiciones de equilibrio pueden clasificarse en estables o inestables (hay más casos, cuando se considera la dependencia respecto a varias variables, pero aquí, por simplicidad, consideraremos solo una variable).
Consideremos, por ejemplo, un péndulo simple formado por una masa que cuelga de un punto de anclaje sujeto por una barra rígida sin masa. Este sistema posee dos posiciones de equilibrio: que la masa está en el punto más bajo del péndulo, o que esté en el punto más alto. Es claro que las dos posiciones no son equivalentes. Mientras que en la posición inferior la masa tiende a permanecer en ella, si se encuentra en el extremo superior cualquier pequeña perturbación hace que la masa caiga.
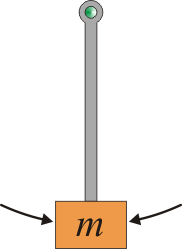
| 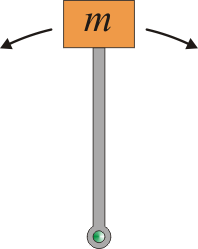
|
| Estable | Inestable |
|---|
Los puntos de equilibrio se clasifican en:
- Estables
- Ante una pequeña perturbación, tienden a retornar a la posición de equilibrio. El ejemplo representativo lo supone una partícula que rueda dentro de un cuenco, o una masa sujeta a un resorte.
- Inestables
- Una pequeña perturbación separa a la masa del equilibrio, y ésta tiende a alejarse de esta posición. Es el caso de una masa situada en lo alto de una cima o del péndulo invertido. También es el caso de una partícula en el interior de un tubo en rotación. Cuando se separa del centro, la inexistencia de una fuerza centrípeta hace que se aleje aun más.
- Indiferente
- La partícula no tiende a retornar a la posición de equilibrio, pero tampoco a alejarse de ella. Es el caso de una bola situada sobre una mesa horizontal.
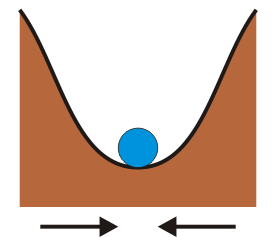
| 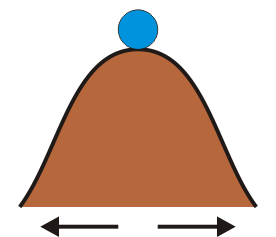
| 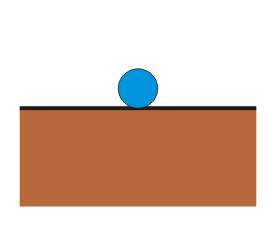
|
| Estable | Inestable | Indiferente |
|---|
La clasificación se complica en 3 dimensiones por el hecho de que una posición de equilibrio puede ser estable respecto a fuerzas aplicadas en una dirección e inestable frente a otras aplicadas en una diferente.
También puede ocurrir que una misma posición de equilibrio pueda ser estable para ciertos valores de los parámetros (por ejemplo, la masa de la partícula) e inestable para valores diferentes.
En términos de la energía potencial, se trata de ver:
- Si U tiene un mínimo es una posición de equilibrio estable.
- Si U tiene un máximo es una posición de equilibrio inestable.
Cuando la energía es una función derivable se puede emplear el criterio de la segunda derivada: si es positiva se trata de un mínimo (equilibrio estable) y si es negativa se trata de un máximo (equilibrio inestable).
En el caso del equilibrio estable sin rozamiento, una partícula que esté cerca de la poisición de equilibrio oscilará alrededor de esta. Podemos calcular la frecuencia de estas oscilaciones con ayuda de la serie de Taylor
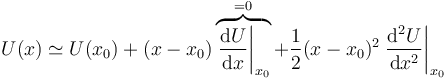
La primera derivada se anula porque la fuerza es nula en la posición de equilibrio. De forma más corta queda
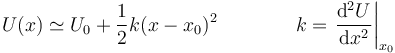
Esta es la energía de un oscilador armónico de frecuencia

Más en general, si la posición se determina por una variable θ tal que la energía cinética se puede escribir

la frecuencia de las oscilaciones es
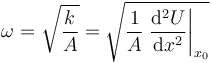
Así, para el péndulo simple tenemos
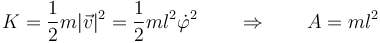
y
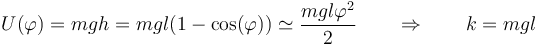
resultando la frecuencia