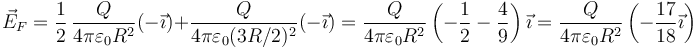Dos esferas cargadas adyacentes
De Laplace
| Línea 27: | Línea 27: | ||
El punto <math>A(-R,0)</math> es el centro de la esfera izquierda, por tanto el campo que produce ella misma es nulo. Este punto se encuentra en el exterior de la esfera derecha, a una distancia 2R de su centro. El unitario radial respecto a esta esfera es <math>-\vec{\imath}</math>. Por ello | El punto <math>A(-R,0)</math> es el centro de la esfera izquierda, por tanto el campo que produce ella misma es nulo. Este punto se encuentra en el exterior de la esfera derecha, a una distancia 2R de su centro. El unitario radial respecto a esta esfera es <math>-\vec{\imath}</math>. Por ello | ||
| - | <center><math>\vec{E}_A=\vec{0} +\frac{Q}{4\pi\varepsilon_0(2R)^2}(-\vec{\imath})=\frac{Q}{4\pi\varepsilon_0R^2}\left(-\frac{1}{4}\vec{\imath})</math></center> | + | <center><math>\vec{E}_A=\vec{0} +\frac{Q}{4\pi\varepsilon_0(2R)^2}(-\vec{\imath})=\frac{Q}{4\pi\varepsilon_0R^2}\left(-\frac{1}{4}\vec{\imath}\right)</math></center> |
===Punto B=== | ===Punto B=== | ||
El punto B es el simétrico del A. Por la simetría del sistema, el campo será igual en magnitud y opuesto al anterior, es decir | El punto B es el simétrico del A. Por la simetría del sistema, el campo será igual en magnitud y opuesto al anterior, es decir | ||
| - | <center><math>\vec{E}_A=\frac{Q}{4\pi\varepsilon_0(2R)^2}(+\vec{\imath})+\vec{0}=\frac{Q}{4\pi\varepsilon_0R^2}\left(\frac{1}{4}\vec{\imath})</math></center> | + | <center><math>\vec{E}_A=\frac{Q}{4\pi\varepsilon_0(2R)^2}(+\vec{\imath})+\vec{0}=\frac{Q}{4\pi\varepsilon_0R^2}\left(\frac{1}{4}\vec{\imath}\right)</math></center> |
===Punto C=== | ===Punto C=== | ||
| Línea 51: | Línea 51: | ||
<center><math>\vec{E}_C=\frac{Q}{4\pi\varepsilon_0(5R/3)^2}\left(\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{\jmath}-\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{\jmath}\right)=\frac{Q}{4\pi\varepsilon_0R^2}\left(\frac{72}{125}\vec{\jmath}\right)</math></center> | <center><math>\vec{E}_C=\frac{Q}{4\pi\varepsilon_0(5R/3)^2}\left(\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{\jmath}-\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{\jmath}\right)=\frac{Q}{4\pi\varepsilon_0R^2}\left(\frac{72}{125}\vec{\jmath}\right)</math></center> | ||
| - | Vemos que las componentes paralelas al eje X se anulan y solo quedan las verticales, que son iguales | + | Vemos que las componentes paralelas al eje X se anulan y solo quedan las verticales, que son iguales. |
| + | |||
| + | ===Punto D=== | ||
| + | Este también está fuera de las dos esferas, pero a diferente distancia de los dos centros. El vector unitario es <math>-\vec{\imath}</math> para las dos esferas. Por ello | ||
| + | |||
| + | <center><math>\vec{E}_D=\frac{Q}{4\pi\varepsilon_0(5R/3)^2}(-\vec{\imath})+\frac{Q}{4\pi\varepsilon_0(11R/3)^2}(-\vec{\imath})=\frac{Q}{4\pi\varepsilon_0R^2}\left(-\frac{9}{25}-\frac{9}{121}\right)\vec{\imath}=\frac{Q}{4\pi\varepsilon_0R^2}\left(-\frac{1314}{3025}\vec{\imath}\right)</math></center> | ||
| + | |||
| + | ===Punto F=== | ||
| + | Por último, el punto F se halla fuera de la esfera derecha, pero dentro de la izquierda. El campo de la derecha es el de una carga puntual. El de la esfera izquierda varía linealmente desde el centro a la superficie. Puesto que F se encuentra a una distancia R/2 del centro, su campo será la mitad del de la superficie. Por tanto | ||
| + | |||
| + | <center><math>\vec{E}_F=\frac{1}{2}\,\frac{Q}{4\pi\varepsilon_0R^2}(-\vec{\imath})+\frac{Q}{4\pi\varepsilon_0(3R/2)^2}(-\vec{\imath})=\frac{Q}{4\pi\varepsilon_0R^2}\left(-\frac{1}{2}-\frac{4}{9}\right)\vec{\imath}=\frac{Q}{4\pi\varepsilon_0R^2}\left(-\frac{17}{18}\vec{\imath}\right)</math></center> | ||
==Trabajo en el primer camino== | ==Trabajo en el primer camino== | ||
==Trabajo en el segundo camino== | ==Trabajo en el segundo camino== | ||
Revisión de 22:26 9 sep 2016
Contenido |
1 Enunciado
Dos esferas de radio R están cargadas uniformemente en su volumen con una carga Q cada una. Las dos esferas son adyacentes, de forma que sus centros se hallan en 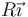 .
.

- Calcule el campo eléctrico en los puntos A( − R,0), B( + R,0), C(0,4R3), D( − 8R3,0) y F( − 3R2,0). El campo en todos estos puntos puede escribirse en la forma

- con
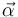 un cierto coeficiente vectorial distinto para cada punto, que es el que hay que determinar.
un cierto coeficiente vectorial distinto para cada punto, que es el que hay que determinar.
- Calcule el trabajo necesario para mover una cierta carga puntual q desde el punto A al punto B, si la carga se desplaza lentamente a lo largo del segmento rectilíneo indicado.
- Calcule el trabajo necesario para mover la misma carga puntual q desde el punto C al punto D, si la carga se desplaza lentamente a lo largo del camino quebrado que se indica.
2 Campo eléctrico
El campo eléctrico puede hallarse como la superposición del que crea cada esfera.
Asimismo, el campo creado por una esfera cargada uniformemente en volumen es en su exterior igual al de una carga puntual y en su interior varía linealmente con la distancia, desde 0 en el centro hasta el valor máximo en la superficie.
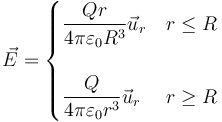
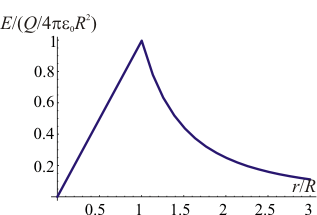
Aquí, r es la distancia al centro de la esfera (no al origen de coordenadas) y 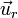 es el vector unitario radial hacia afuera de ella.
es el vector unitario radial hacia afuera de ella.
Teniendo esto en cuenta, quedan los resultados siguientes:
2.1 Punto A
El punto A( − R,0) es el centro de la esfera izquierda, por tanto el campo que produce ella misma es nulo. Este punto se encuentra en el exterior de la esfera derecha, a una distancia 2R de su centro. El unitario radial respecto a esta esfera es 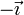 . Por ello
. Por ello
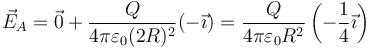
2.2 Punto B
El punto B es el simétrico del A. Por la simetría del sistema, el campo será igual en magnitud y opuesto al anterior, es decir
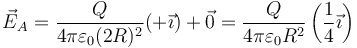
2.3 Punto C
Este punto se halla en el exterior de las dos esferas, es decir, el campo será la suma del de dos carga puntuales. La distancia a los dos centros es la misma, siendo esta distancia
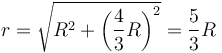
El vector unitario desde el centro de la esfera izquierda es
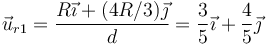
y, desde la esfera derecha, por simetría
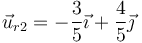
Esto nos da el campo
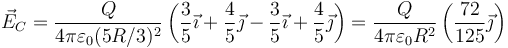
Vemos que las componentes paralelas al eje X se anulan y solo quedan las verticales, que son iguales.
2.4 Punto D
Este también está fuera de las dos esferas, pero a diferente distancia de los dos centros. El vector unitario es 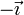 para las dos esferas. Por ello
para las dos esferas. Por ello
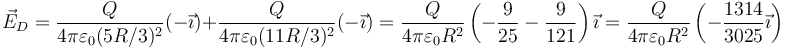
2.5 Punto F
Por último, el punto F se halla fuera de la esfera derecha, pero dentro de la izquierda. El campo de la derecha es el de una carga puntual. El de la esfera izquierda varía linealmente desde el centro a la superficie. Puesto que F se encuentra a una distancia R/2 del centro, su campo será la mitad del de la superficie. Por tanto