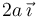No Boletín - Dos varillas (Ex.Ene/16)
De Laplace
(→Vector de posición del C.I.R. del movimiento {20}) |
(→Velocidad {20} del punto O) |
||
| Línea 17: | Línea 17: | ||
==Velocidad {20} del punto O== | ==Velocidad {20} del punto O== | ||
| - | <math>-\,a | + | <math>-\,a\dot{\theta}\,\vec{\jmath}\,</math> |
==Vector de posición del C.I.R. del movimiento {20}== | ==Vector de posición del C.I.R. del movimiento {20}== | ||
Revisión de 12:07 1 ene 2006
Contenido |
1 Enunciado
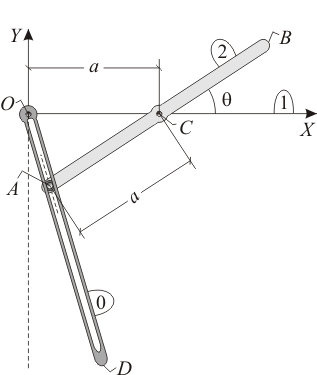
El sistema mecánico de la figura está constituido por dos varillas móviles, 
(sólido "2") y 
(sólido 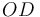"0"), ambas de grosor despreciable e igual longitud 
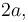y contenidas siempre en el plano fijo 
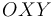(sólido "1"). Cada varilla se encuentra articulada en un punto fijo: la primera en su centro 
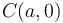y la segunda en su extremo 
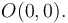Además, ambas varillas se mueven vinculadas entre sí porque la varilla 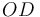posee una
acanaladura longitudinal por la cual desliza el extremo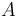 
de la varilla 
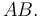Se utiliza el ángulo 
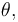formado por la varilla y el eje 
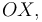como parámetro descriptivo del movimiento del
sistema.
Nota: Obsérvese que, con ayuda del triángulo isósceles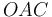 
de la figura, se puede determinar (en función de 
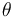) el ángulo formado por la varilla 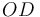y el eje 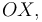o también el ángulo formado por ambas varillas.
Determine las siguientes magnitudes:
- Velocidad angular
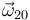
- Velocidad
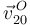
- Vector de posición
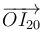del centro instantáneo de rotación del movimiento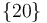 
2 Velocidad angular del movimiento {20}
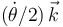
3 Velocidad {20} del punto O
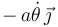
4 Vector de posición del C.I.R. del movimiento {20}
