No Boletín - Dos varillas (Ex.Ene/16)
De Laplace
Contenido |
1 Enunciado
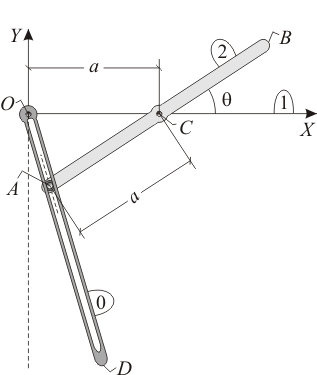
El sistema mecánico de la figura está constituido por dos varillas móviles,  (sólido "2") y
(sólido "2") y  (sólido "0"), ambas de grosor despreciable e igual longitud
(sólido "0"), ambas de grosor despreciable e igual longitud 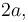 y contenidas siempre en el plano fijo
y contenidas siempre en el plano fijo 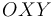 (sólido "1"). Cada varilla se encuentra articulada en un punto fijo: la primera en su centro
(sólido "1"). Cada varilla se encuentra articulada en un punto fijo: la primera en su centro 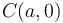 y la segunda en su extremo
y la segunda en su extremo 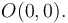 Además, ambas varillas se mueven vinculadas entre sí porque la varilla
Además, ambas varillas se mueven vinculadas entre sí porque la varilla 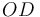 posee una
acanaladura longitudinal por la cual desliza el extremo
posee una
acanaladura longitudinal por la cual desliza el extremo 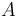 de la varilla
de la varilla 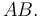 Se utiliza el ángulo
Se utiliza el ángulo 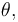 formado por la varilla
formado por la varilla  y el eje
y el eje 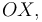 como parámetro descriptivo del movimiento del
sistema.
como parámetro descriptivo del movimiento del
sistema.
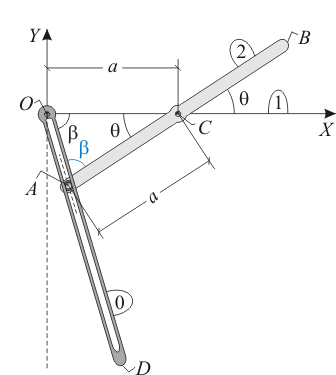
Nota: Obsérvese que, con ayuda del triángulo isósceles 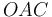 de la figura, se puede determinar (en función de
de la figura, se puede determinar (en función de 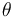 ) el ángulo formado por la varilla
) el ángulo formado por la varilla 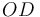 y el eje
y el eje 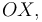 o también el ángulo formado por ambas varillas.
o también el ángulo formado por ambas varillas.
Determine las siguientes magnitudes:
- Velocidad angular
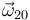
- Velocidad
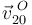
- Vector de posición
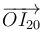 del centro instantáneo de rotación del movimiento
del centro instantáneo de rotación del movimiento 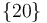
2 Velocidad angular del movimiento {20}
Exigiendo que la suma de todos los ángulos internos del triángulo isósceles 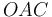 sea
sea 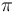 radianes, determinamos el ángulo
radianes, determinamos el ángulo 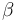 (en color azul en la figura adjunta) que forman ambas varillas entre sí:
(en color azul en la figura adjunta) que forman ambas varillas entre sí:

Al ser 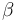 el ángulo que forma la varilla
el ángulo que forma la varilla  (sólido "2") con respecto a la varilla
(sólido "2") con respecto a la varilla 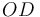 (sólido "0"), la velocidad angular
(sólido "0"), la velocidad angular 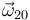 puede expresarse así:
puede expresarse así:
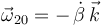
donde el signo negativo se justifica mediante el siguiente razonamiento: si el ángulo 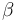 que forma la varilla "2" respecto a la varilla "0" aumenta (
que forma la varilla "2" respecto a la varilla "0" aumenta (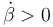 ), la rotación
), la rotación  es horaria (
es horaria (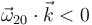 ). Ampliando este razonamiento a la situación inversa, podemos resumir la justificación del signo negativo en la necesidad de garantizar las siguientes correspondencias:
). Ampliando este razonamiento a la situación inversa, podemos resumir la justificación del signo negativo en la necesidad de garantizar las siguientes correspondencias:

Sustituyendo la expresión de 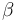 obtenida al principio, determinamos
obtenida al principio, determinamos 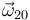 :
:
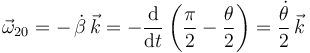
3 Velocidad {20} del punto O
Empezaremos calculando la velocidad 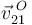 , y para ello vamos a determinar previamente la reducción cinemática
, y para ello vamos a determinar previamente la reducción cinemática  en el punto
en el punto  . Elegimos
. Elegimos 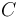 como centro de reducción
como centro de reducción  porque la varilla "2" se halla articulada en dicho punto, y por tanto
porque la varilla "2" se halla articulada en dicho punto, y por tanto 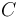 es un punto fijo en el movimiento
es un punto fijo en el movimiento  :
:
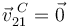
Al ser 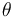 el ángulo que forma la varilla
el ángulo que forma la varilla  (sólido "2") con respecto al eje
(sólido "2") con respecto al eje 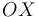 (sólido "1"), la velocidad angular
(sólido "1"), la velocidad angular 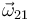 puede expresarse así:
puede expresarse así:
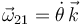
donde el signo positivo (que se omite) delante de 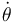 se justifica mediante el siguiente razonamiento: si el ángulo
se justifica mediante el siguiente razonamiento: si el ángulo 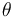 que forma la varilla "2" con respecto al eje
que forma la varilla "2" con respecto al eje 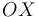 del sólido "1" aumenta (
del sólido "1" aumenta (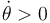 ), la rotación
), la rotación  es antihoraria (
es antihoraria (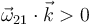 ). Ampliando este razonamiento a la situación inversa, cabe resumir la justificación del signo positivo en la necesidad de garantizar las siguientes correspondencias:
). Ampliando este razonamiento a la situación inversa, cabe resumir la justificación del signo positivo en la necesidad de garantizar las siguientes correspondencias:

Conocida la reducción cinemática 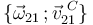 , ya podemos calcular la velocidad
, ya podemos calcular la velocidad 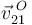 mediante la ecuación del campo de velocidades
mediante la ecuación del campo de velocidades  :
:
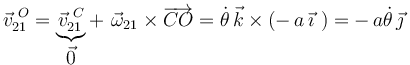
Por otra parte, el punto  es un punto fijo en el movimiento
es un punto fijo en el movimiento  porque la varilla "0" se halla articulada en él:
porque la varilla "0" se halla articulada en él:
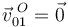
Conocidas las velocidades 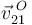 y
y 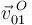 , la ley de composición de velocidades nos permite determinar la velocidad
, la ley de composición de velocidades nos permite determinar la velocidad 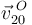 :
:
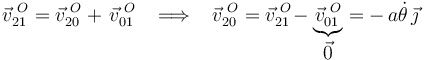
4 Vector de posición del C.I.R. del movimiento {20}
La posición del centro instantáneo de rotación 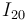 respecto al origen de coordenadas
respecto al origen de coordenadas  se puede determinar ANALÍTICAMENTE mediante la fórmula:
se puede determinar ANALÍTICAMENTE mediante la fórmula:
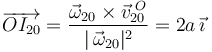
El vector de posición 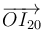 obtenido es constante (no depende del parámetro
obtenido es constante (no depende del parámetro  descriptivo del movimiento del sistema). Por tanto,
descriptivo del movimiento del sistema). Por tanto, 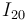 es en realidad un centro permanente de rotación.
es en realidad un centro permanente de rotación.
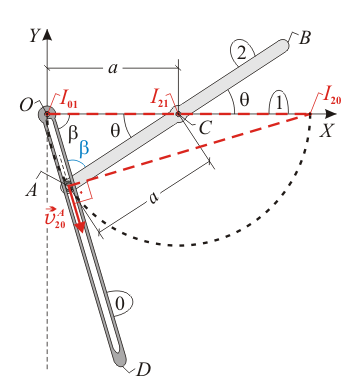
También es posible determinar la posición de 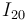 GRÁFICAMENTE.
GRÁFICAMENTE.
Para ello, localizamos primero los centros permanentes de rotación  e
e 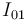 , que coinciden con los puntos de articulación de las varillas "2" y "0", respectivamente:
, que coinciden con los puntos de articulación de las varillas "2" y "0", respectivamente:

En cuanto al movimiento 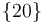 , se nos indica que el extremo
, se nos indica que el extremo  de la varilla "2" está obligado a recorrer la acanaladura longitudinal de la varilla "0", lo cual nos permite saber que la velocidad
de la varilla "2" está obligado a recorrer la acanaladura longitudinal de la varilla "0", lo cual nos permite saber que la velocidad 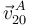 es necesariamente colineal con la propia varilla "0". Trazando la perpendicular a dicha velocidad en el punto
es necesariamente colineal con la propia varilla "0". Trazando la perpendicular a dicha velocidad en el punto  y trazando la recta que pasa por los puntos
y trazando la recta que pasa por los puntos 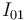 e
e 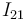 (en aplicación del teorema de los tres centros), hallaremos el punto
(en aplicación del teorema de los tres centros), hallaremos el punto 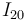 en la intersección de ambas rectas:
en la intersección de ambas rectas:

Por último, subrayemos la obligada coincidencia de resultados entre el procedimiento analítico y el procedimiento gráfico utilizados para determinar la posición de 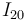 . Nótese que el punto
. Nótese que el punto 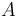 recorre en su movimiento absoluto una circunferencia de radio
recorre en su movimiento absoluto una circunferencia de radio 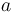 y centro en
y centro en 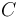 (marcada con línea negra discontinua en la figura adjunta). El punto
(marcada con línea negra discontinua en la figura adjunta). El punto 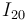 se sitúa sobre dicha circunferencia y en la posición diametralmente opuesta a la posición del punto
se sitúa sobre dicha circunferencia y en la posición diametralmente opuesta a la posición del punto  , de tal modo que el diámetro fijo
, de tal modo que el diámetro fijo 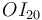 es "visto" siempre bajo un ángulo de 90º desde el punto
es "visto" siempre bajo un ángulo de 90º desde el punto 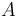 con independencia de la posición concreta de este último sobre la circunferencia (arco capaz de 90º).
con independencia de la posición concreta de este último sobre la circunferencia (arco capaz de 90º).