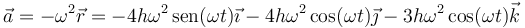Ejemplo de movimiento armónico tridimensional
De Laplace
(Diferencias entre revisiones)
| Línea 2: | Línea 2: | ||
Una partícula se mueve de forma que en todo momento verifica la ecuación del oscilador armónico en tres dimensiones | Una partícula se mueve de forma que en todo momento verifica la ecuación del oscilador armónico en tres dimensiones | ||
| - | <center><math>\vec{a}=-\omega^2 \vec{r} | + | <center><math>\vec{a}=-\omega^2 \vec{r}</math></center> |
| - | </math></center> | + | |
siendo su posición y velocidad iniciales | siendo su posición y velocidad iniciales | ||
| Línea 26: | Línea 25: | ||
Sustituimos los datos del enunciado y queda | Sustituimos los datos del enunciado y queda | ||
| - | <center><math>\vec{r}=\left(4h\vec{\jmath}+3h\vec{k}\right)\cos(\omega t)+\left(4h\vec{\imath}\right)\mathrm{sen}(\omega t) | + | <center><math>\vec{r}=\left(4h\vec{\jmath}+3h\vec{k}\right)\cos(\omega t)+\left(4h\vec{\imath}\right)\mathrm{sen}(\omega t) |
= 4h\,\mathrm{sen}(\omega t)\vec{\imath}+4h\cos(\omega t)\vec{\jmath}+3h\cos(\omega t)\vec{k}</math></center> | = 4h\,\mathrm{sen}(\omega t)\vec{\imath}+4h\cos(\omega t)\vec{\jmath}+3h\cos(\omega t)\vec{k}</math></center> | ||
| + | ===Velocidad=== | ||
| + | Una vez que tenemos la posición instantánea, calculamos la velocidad instantánea derivando respecto al tiempo | ||
| + | |||
| + | <center><math>\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=4h\omega\cos(\omega t)\vec{\imath}-4h\omega\,\mathrm{sen}(\omega t)\vec{\jmath}-3h\omega\,\mathrm{sen}(\omega t)\vec{k}</math></center> | ||
| + | |||
| + | ===Aceleración=== | ||
| + | Para hallar la aceleración podemos derivar de nuevo o usar la ecuación del oscilador armónico | ||
| + | |||
| + | <center><math>\vec{a}=-\omega^2 \vec{r}=-4h\omega^2\,\mathrm{sen}(\omega t)\vec{\imath}-4h\omega^2\cos(\omega t)\vec{\jmath}-3h\omega^2\cos(\omega t)\vec{k}</math></center> | ||
[[Categoría:Problemas de cinemática tridimensional (GIE)|0]] | [[Categoría:Problemas de cinemática tridimensional (GIE)|0]] | ||
[[Categoría:Problemas de cinemática de la partícula (GIE)]] | [[Categoría:Problemas de cinemática de la partícula (GIE)]] | ||
Revisión de 17:27 9 nov 2015
Contenido |
1 Enunciado
Una partícula se mueve de forma que en todo momento verifica la ecuación del oscilador armónico en tres dimensiones
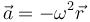
siendo su posición y velocidad iniciales

- Calcule la posición, velocidad y aceleración de la partícula en todo instante.
- Para el instante t = 0 halle:
- El triedro de Frenet:
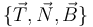 .
.
- Las componentes intrínsecas de la aceleración (en forma escalar y vectorial).
- La posición del centro de curvatura.
- El triedro de Frenet:
- Empleando coordenadas cilíndricas y su base asociada:
- Escriba las ecuaciones horarias
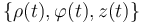 .
.
- Escriba los vectores de posición, velocidad y aceleración como función del tiempo.
- Escriba las ecuaciones horarias
- Identifique este movimiento: ¿Es plano? ¿Es rectilíneo? ¿Es uniforme? ¿Cómo es la trayectoria? Justifique las respuestas.
2 Posición, velocidad y aceleración
2.1 Posición
En un oscilador armónico tridimensional, la solución general para la posición es de la forma
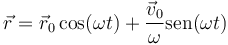
Sustituimos los datos del enunciado y queda
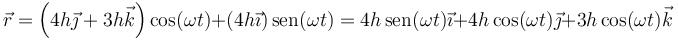
2.2 Velocidad
Una vez que tenemos la posición instantánea, calculamos la velocidad instantánea derivando respecto al tiempo
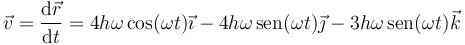
2.3 Aceleración
Para hallar la aceleración podemos derivar de nuevo o usar la ecuación del oscilador armónico