Divergencia de un campo vectorial
De Laplace
(→Fuentes escalares de un campo vectorial) |
(→Fuentes escalares de un campo vectorial) |
||
| Línea 51: | Línea 51: | ||
Ambos, manantiales y sumideros, constituyen las ''fuentes escalares'' de un campo vectorial; por ello | Ambos, manantiales y sumideros, constituyen las ''fuentes escalares'' de un campo vectorial; por ello | ||
| - | * Si la divergencia es nula en un punto el campo | + | * Si la divergencia es nula en un punto el campo ''carece de fuentes escalares'' en dicho punto. |
El concepto de divergencia se define para cada punto. A partir de esta definición, puede construirse un campo escalar a partir de uno vectorial, | El concepto de divergencia se define para cada punto. A partir de esta definición, puede construirse un campo escalar a partir de uno vectorial, | ||
Revisión de 19:49 30 dic 2008
Contenido |
1 Introducción
2 Definición
Se define la divergencia de un campo vectorial  en un punto
en un punto  como el límite
como el límite
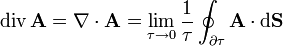
donde el límite se toma sobre volúmenes τ cada vez más pequeños que tienden al punto 
La divergencia de un campo vectorial es una cantidad escalar.
Esta cantidad es independiente de la sucesión de volúmenes que se tomen con tal de que converjan en el mismo punto de manera uniforme.
2.1 Ejemplo
Vamos a calcular la divergencia de 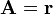 en
en 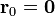 .
.
En el artículo sobre flujo de un campo vectorial se ve que si consideramos una superficie cúbica de arista 2a en torno al origen de coordenadas, el flujo del vector de posición a través de esta superficie es
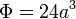
El volumen de este cubo es
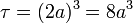
Por tanto la divergencia en 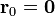 es
es
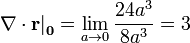
Calculemos ahora esta misma divergencia pero considerando esferas de radio R en torno al origen. Para cada una de estas esferas el volumen es
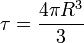
y el flujo a través de la superficie esférica
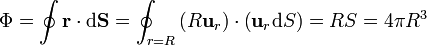
por lo que la divergencia en 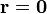 es
es
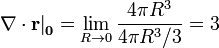
Vemos que el resultado es independiente de que lo hayamos calculado usando cubos o esferas.
Hay que destacar que lo que hemos calculado es la divergencia en un solo punto.
3 Fuentes escalares de un campo vectorial
La divergencia es una cantidad escalar con signo. Este signo posee significado geométrico y físico:
- Si la divergencia de un campo vectorial en un punto es positiva, quiere decir que en dicho punto el campo mana hacia el exterior. Se dice que esa posición el campo vectorial posee un manantial.
- Si por contra la divergencia es negativa, el campo converge hacia dicho punto; se dice que el campo posee un sumidero.
Ambos, manantiales y sumideros, constituyen las fuentes escalares de un campo vectorial; por ello
- Si la divergencia es nula en un punto el campo carece de fuentes escalares en dicho punto.
El concepto de divergencia se define para cada punto. A partir de esta definición, puede construirse un campo escalar a partir de uno vectorial,





