Divergencia de un campo vectorial
De Laplace
(Diferencias entre revisiones)
(→Definición) |
(→Definición) |
||
| Línea 4: | Línea 4: | ||
<center><math>\mathrm{div}\,\mathbf{A}=\nabla\cdot\mathbf{A}=\lim_{\tau\to 0}\frac{1}{\tau} \oint_{\partial\tau}\mathbf{A}\cdot\mathrm{d}\mathbf{S}</math></center> | <center><math>\mathrm{div}\,\mathbf{A}=\nabla\cdot\mathbf{A}=\lim_{\tau\to 0}\frac{1}{\tau} \oint_{\partial\tau}\mathbf{A}\cdot\mathrm{d}\mathbf{S}</math></center> | ||
| + | |||
| + | donde el límite se toma sobre volúmenes <math>\tau</math> cada vez más pequeños que tienden al punto <math>\mathbf{r}_0</math> | ||
==Fuentes escalares de un campo vectorial== | ==Fuentes escalares de un campo vectorial== | ||
Revisión de 18:32 30 dic 2008
Contenido |
1 Introducción
2 Definición
Se define la divergencia de un campo vectorial 
en un punto 
como el límite
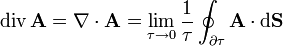
donde el límite se toma sobre volúmenes τ cada vez más pequeños que tienden al punto
