Movimiento circular con aceleraciones relacionadas
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula describe un movimiento circular en el plano XY alrededor del origen de coordenadas de tal forma que en todo instante se cumple la relación entre la…') |
(→Enunciado) |
||
| Línea 5: | Línea 5: | ||
Inicialmente la partícula se encuentra en <math>R\vec{\imath}</math>, moviéndose con velocidad <math>v_0\vec{\jmath}</math> | Inicialmente la partícula se encuentra en <math>R\vec{\imath}</math>, moviéndose con velocidad <math>v_0\vec{\jmath}</math> | ||
| - | # Para el instante <math>t=0</math>, halle el vector aceleración, el vector velocidad | + | # Para el instante <math>t=0</math>, halle el vector aceleración, el vector velocidad angular y el vector aceleración angular. |
| - | angular y el vector aceleración angular. | + | |
# Calcule la rapidez de la partícula como función del tiempo. | # Calcule la rapidez de la partícula como función del tiempo. | ||
# Halle la distancia recorrida, así como el ángulo <math>\varphi</math> que el vector de posición forma con el eje OX, como función del tiempo | # Halle la distancia recorrida, así como el ángulo <math>\varphi</math> que el vector de posición forma con el eje OX, como función del tiempo | ||
[[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | [[Categoría:Problemas de cinemática tridimensional de la partícula (GIE)]] | ||
Revisión de 19:56 3 feb 2015
Enunciado
Una partícula describe un movimiento circular en el plano XY alrededor del origen de coordenadas de tal forma que en todo instante se cumple la relación entre las componentes intrínsecas escalares de la aceleración:
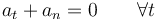
Inicialmente la partícula se encuentra en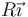 
, moviéndose con velocidad 
- Para el instante t = 0, halle el vector aceleración, el vector velocidad angular y el vector aceleración angular.
- Calcule la rapidez de la partícula como función del tiempo.
- Halle la distancia recorrida, así como el ángulo
que el vector de posición forma con el eje OX, como función del tiempo
