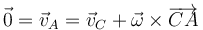Bola que rueda por una pendiente
De Laplace
| Línea 13: | Línea 13: | ||
==Introducción== | ==Introducción== | ||
| - | Este problema es una consecuencia inmediata de lo que se discute en teoría sobre rodadura | + | Este problema es una consecuencia inmediata de lo que se discute en teoría sobre [[Sistemas_simples_de_s%C3%B3lidos_r%C3%ADgidos#Rodadura|rodadura]], siendo en este caso la fuerza aplicada la componente útil del peso (la tangencial al plano). |
| + | |||
==Relación entre aceleraciones== | ==Relación entre aceleraciones== | ||
| + | Elegimos un sistema de ejes en el que el eje OX es el tangencial al plano en la dirección de descenso, OY el normal al plano hacia fuera de él y OZ el perpendicular a la figura y en el sentido hacia afuera de ésta (o de la pantalla). | ||
| + | |||
| + | En este sistema, la velocidad y la aceleración del CM es en la dirección de movimiento, es decir | ||
| + | |||
| + | <center><math>\vec{v}_C=v_C\vec{\imath}\qquad\qquad \vec{a}_C = a_C\vec{\imath}</math></center> | ||
| + | |||
| + | mientras que la velocidad y la aceleración angular son perpendiculares al plano de la figura | ||
| + | |||
| + | <center><math>\vec{\omega}=\omega\vec{k}\qquad \vec{\alpha}=\alpha\vec{k}</math></center> | ||
| + | |||
| + | Por estar rodando sin deslizar, se anula la velocidad del punto A de contacto entre la bola y el suelo. | ||
| + | <center><math>\vec{0}=\vec{v}_A=\vec{v}_C+\vec{\omega}\times\overrightarrow{CA}</math></center> | ||
==Energías== | ==Energías== | ||
==Aceleración== | ==Aceleración== | ||
==Coeficiente de rozamiento mínimo== | ==Coeficiente de rozamiento mínimo== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 19:01 29 ene 2015
Contenido |
1 Enunciado
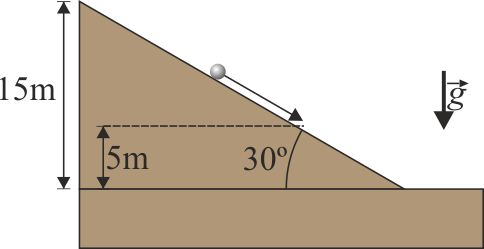
Una esfera metálica de acero con radio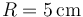 
) se encuentra inicialmente en reposo a una altura 
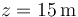y desciende rodando sin deslizar por el plano inclinado con un ángulo 
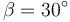. El coeficiente de rozamiento estático entre el plano y el cilindro es μ. El rozamiento por rodadura es despreciable.
- ¿Qué relación existe entre la aceleración angular de la esfera y la lineal de su centro de masas?
- ¿Cuánto valen la energía cinética de rotación, la cinética de traslación, la potencial (tomando z = 0 como referencia) y la mecánica cuando se halla en
?
- ¿Cuánto vale, en módulo, la aceleración lineal del centro de masas de la esfera?
- ¿Cuál es el valor mínimo que debe tener el coeficiente de rozamiento μ si la esfera rueda sin deslizar?
Dato: Momento de inercia de una esfera de masa M y radio R respecto a un eje que pasa por su centro: I = (2 / 5)MR2. Aceleración de
la gravedad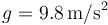 
. Densidad de masa del acero: 
.
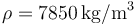2 Introducción
Este problema es una consecuencia inmediata de lo que se discute en teoría sobre rodadura, siendo en este caso la fuerza aplicada la componente útil del peso (la tangencial al plano).
3 Relación entre aceleraciones
Elegimos un sistema de ejes en el que el eje OX es el tangencial al plano en la dirección de descenso, OY el normal al plano hacia fuera de él y OZ el perpendicular a la figura y en el sentido hacia afuera de ésta (o de la pantalla).
En este sistema, la velocidad y la aceleración del CM es en la dirección de movimiento, es decir
mientras que la velocidad y la aceleración angular son perpendiculares al plano de la figura
Por estar rodando sin deslizar, se anula la velocidad del punto A de contacto entre la bola y el suelo.
