Bola que rueda por una pendiente
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una esfera metálica de acero con radio <math>R=5\,\mathrm{cm}</math>) se encuentra inicialmente en reposo a una altura <math>z=15\,\mathrm{m}</math> y desciende r…') |
|||
| Línea 12: | Línea 12: | ||
la gravedad <math>g = 9.8\,\mathrm{m}/\mathrm{s}^2</math>. Densidad de masa del acero: <math>\rho = 7850\,\mathrm{kg}/\mathrm{m}^3</math>. | la gravedad <math>g = 9.8\,\mathrm{m}/\mathrm{s}^2</math>. Densidad de masa del acero: <math>\rho = 7850\,\mathrm{kg}/\mathrm{m}^3</math>. | ||
| + | ==Introducción== | ||
| + | Este problema es una consecuencia inmediata de lo que se discute en teoría sobre rodadura | ||
==Relación entre aceleraciones== | ==Relación entre aceleraciones== | ||
| + | |||
==Energías== | ==Energías== | ||
==Aceleración== | ==Aceleración== | ||
==Coeficiente de rozamiento mínimo== | ==Coeficiente de rozamiento mínimo== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 18:52 29 ene 2015
Contenido |
1 Enunciado
Una esfera metálica de acero con radio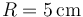 
) se encuentra inicialmente en reposo a una altura 
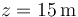y desciende rodando sin deslizar por el plano inclinado con un ángulo 
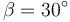. El coeficiente de rozamiento estático entre el plano y el cilindro es μ. El rozamiento por rodadura es despreciable.
- ¿Qué relación existe entre la aceleración angular de la esfera y la lineal de su centro de masas?
- ¿Cuánto valen la energía cinética de rotación, la cinética de traslación, la potencial (tomando z = 0 como referencia) y la mecánica cuando se halla en
?
- ¿Cuánto vale, en módulo, la aceleración lineal del centro de masas de la esfera?
- ¿Cuál es el valor mínimo que debe tener el coeficiente de rozamiento μ si la esfera rueda sin deslizar?
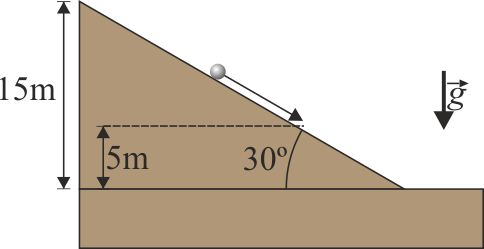
Dato: Momento de inercia de una esfera de masa M y radio R respecto a un eje que pasa por su centro: I = (2 / 5)MR2. Aceleración de
la gravedad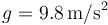 
. Densidad de masa del acero: 
.
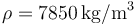2 Introducción
Este problema es una consecuencia inmediata de lo que se discute en teoría sobre rodadura
