Dos esferas huecas
De Laplace
m |
|||
| Línea 1: | Línea 1: | ||
| - | + | ==Enunciado== | |
Se tiene un sistema de cargas formado por dos superficies esféricas de radio <math>b=4\,\mathrm{cm}</math> cuyos centros distan <math>a=3\,\mathrm{cm}</math>, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de <math>+1\,\mathrm{nC}</math> y <math>-1\,\mathrm{nC}</math> | Se tiene un sistema de cargas formado por dos superficies esféricas de radio <math>b=4\,\mathrm{cm}</math> cuyos centros distan <math>a=3\,\mathrm{cm}</math>, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de <math>+1\,\mathrm{nC}</math> y <math>-1\,\mathrm{nC}</math> | ||
| Línea 104: | Línea 104: | ||
|} | |} | ||
==Trabajo== | ==Trabajo== | ||
| + | El trabajo para mover una carga puede hallarse a partir de la diferencia de potencial | ||
| + | <center><math>W_{A\to D) = q(V_D-V_A) = (-10^{-9})(-67.5-45)\,\mathrm{J} = 112.5\,\mathrm{nJ}</math></center> | ||
| + | |||
| + | Sin embargo, aquí se trata de hallarlo a partir de la integración de la fuerza. En un proceso cuasiestático, la fuerza ejercida es opuesta a la eléctrica | ||
| + | |||
| + | <center><math>\vec{F}_\mathrm{ext}=-q\vec{E}</math></center> | ||
| + | |||
| + | y el trabajo que queremos calcular será | ||
| + | |||
| + | <center><math>W=\int_A^D \vec{F}_\mathrm{ext}\cdot\mathrm{d}\vec{r}=-q\int_A^D\vec{E}\cdot \mathrm{d}\vec{r}</math></center> | ||
| + | |||
| + | siendo | ||
| + | |||
| + | <center><math>\mathrm{d}\vec{r}=\mathrm{d}x\,\vec{\imath}\qquad\qquad x\in(-0.02,0.08)</math></center> | ||
| + | |||
| + | A la hora de hacer esta integral tenemos cuatro tramos: | ||
| + | |||
| + | ;Del punto A (x=-0.02) hasta la superficie cargada negativamente (x=-0.01): En este tramo el campo equivale al de una carga puntual situada en el centro de la esfera negativa | ||
| + | |||
| + | <center><math>\vec{E}=\frac{-Q}{4\pi\varepsilon_0 r^2}(-\vec{\imath})= =\frac{9}{(x-0.03)^2}\vec{\imath}</math></center> | ||
| + | |||
| + | :ya que la distancia al centro de la esfera negativa es <math>r = x-0.03</math>. El trabajo para recorrer este trozo es entonces | ||
| + | |||
| + | <center><math>W_1=9\times 10^{-9}\int_{-0.02}^{-0.01} \frac{\mathrm{d}x}{(x-0.03)^2}=9\times 10^{-9} \left.\frac{-1}{x-0.03}\right|_{-0.02}^{0.01} = 45\,\mathrm{nJ}</math></center> | ||
| + | |||
| + | ;Desde la superficie negativa (x=-0.01) hasta la positiva (x=0.04): En estre tramo el campo eléctrico se anula | ||
| + | |||
| + | <center><math>\vec{E}=\vec{0}\qquad\Rightarrow\qquad W_2=0</math></center> | ||
| + | |||
| + | ;Desde la superficie positiva (x=0.04) hasta la negativa (x=0.07): El campo es el de una carga puntual situada en el centro de la esfera positiva | ||
| + | |||
| + | <center><math>\vec{E}=\frac{9}{x^2}\vec{\imath}</math></center> | ||
| + | |||
| + | :siendo el trabajo | ||
| + | |||
| + | <center><math>W_3= 9\times 10^{-9}\int_{0.04}^{0.07}\frac{\mathrm{d}x}{x^2}=96.43\,\mathrm{nJ}</math></center> | ||
| + | |||
| + | ;Desde la superficie negativa (x=0.07) hasta D (x=0.08): Aquí el campo es suma del de dos cargas | ||
| + | |||
| + | <center><math>\vec{E}=9\left(\frac{1}{x^2}-\frac{1}{(x-3)^2}\right)\vec{\imath}</math></center> | ||
| + | |||
| + | :siendo el trabajo | ||
| + | |||
| + | <center><math>W_4 = 9\times 10^{-9}\int_{0.07}^{0.08}\left(\frac{1}{x^2}-\frac{1}{(x-3)^2}\right)\mathrm{d}x = -28.93\,\mathrm{nJ}</math></center> | ||
| + | |||
| + | Sumando las cuatro contribuciones | ||
| + | |||
| + | W = 45+ 96.43 -28.93 = 112.5\mathrm{nJ}\mathrm{nJ} | ||
[[Categoría:Problemas de electrostática en el vacío (GIE)]] | [[Categoría:Problemas de electrostática en el vacío (GIE)]] | ||
Revisión de 21:32 17 jun 2014
Contenido |
1 Enunciado
Se tiene un sistema de cargas formado por dos superficies esféricas de radio 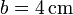 cuyos centros distan
cuyos centros distan 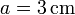 , como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de
, como indica la figura. Las superficies está cargadas uniformemente con cargas respectivas de 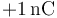 y
y 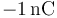
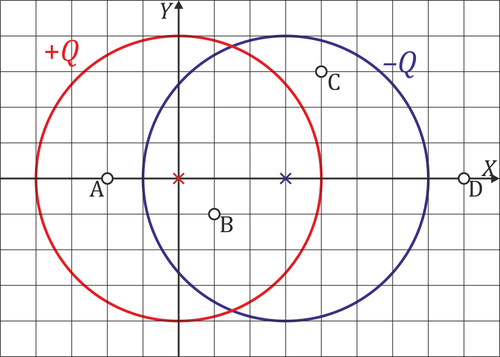
Para los puntos marcados en la figura (en cm)

- Calcule el campo eléctrico.
- Calcule el potencial eléctrico.
- A partir de la integración de la fuerza, halle el trabajo que debe realizar un agente externo para mover cuasiestáticamente una carga de
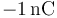 desde el punto A al punto D moviéndola a lo largo del eje X.
desde el punto A al punto D moviéndola a lo largo del eje X.
2 Campo eléctrico
La solución de este problema es una simple aplicación del principio de superposición. Basta con hallar el campo de cada superficie esférica y luego sumar las dos contribuciones.
El campo debido a una superficie esférica de radio acargada uniformemente tiene la expresión
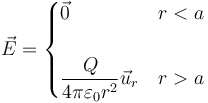
siendo r las distancia del punto de observación al centro de la esfera y 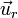 el vector unitario radial hacia afuera.
el vector unitario radial hacia afuera.
En todos los cálculos aparece el mismo factor
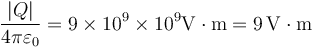
Así, tenemos para los cuatro puntos lo siguiente:
- Punto A
- Este punto está dentro de la esfera de carga positiva y fuera de la negativa. Para esta última la distancia al centro es de 5 cm y el vector unitario radial es
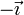 . Por tanto
. Por tanto
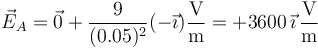
- Punto B
- Se encuentra en el interior de las dos esferas, por lo que
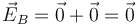
- Punto C
- Éste se halla dentro de la esfera de carga negativa y fuera de la positiva. La distancia al centro de esta es también de 5 cm, pero el unitario radial es ahora el que va en la dirección y sentido del vector
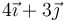
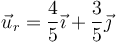
- lo que da el campo
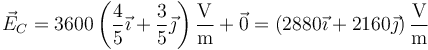
- Punto D
- Por último, este punto se encuentra fuera de las dos esferas, a 8 cm del centro de la esfera positiva y 5 de la negativa. El unitario radial es, en los dos casos
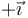 , lo que nos da
, lo que nos da
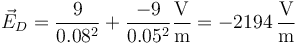
3 Potencial eléctrico
El cálculo para el potencial es análogo. Basta con sumar los potenciales debidos a cada esfera.
El potencial debido a una superficie esférica de radio a cargada uniformemente con una carga Q tiene la expresión
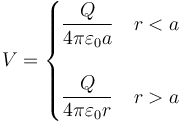
siendo el valor numérico del primer caso
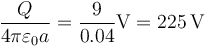
Esto nos da, para los cuatro puntos, siguiendo el mimso razonamiento que para el campo eléctrico
- Punto A
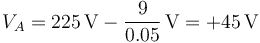
- Punto B
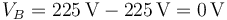
- Punto C
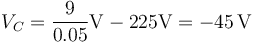
- Punto D
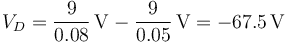
Podemos reunir estos resultados en una tabla
| Punto | 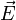 (V/m) (V/m)
| V (V) |
|---|---|---|
| A | 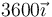
| +45 |
| B | 
| 0 |
| C | 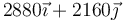
| −45 |
| D | 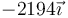
| −67.5 |
4 Trabajo
El trabajo para mover una carga puede hallarse a partir de la diferencia de potencial
Sin embargo, aquí se trata de hallarlo a partir de la integración de la fuerza. En un proceso cuasiestático, la fuerza ejercida es opuesta a la eléctrica
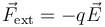
y el trabajo que queremos calcular será
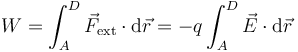
siendo
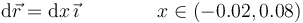
A la hora de hacer esta integral tenemos cuatro tramos:
- Del punto A (x=-0.02) hasta la superficie cargada negativamente (x=-0.01)
- En este tramo el campo equivale al de una carga puntual situada en el centro de la esfera negativa
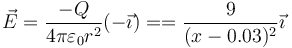
- ya que la distancia al centro de la esfera negativa es r = x − 0.03. El trabajo para recorrer este trozo es entonces
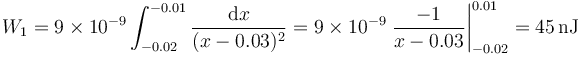
- Desde la superficie negativa (x=-0.01) hasta la positiva (x=0.04)
- En estre tramo el campo eléctrico se anula
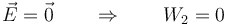
- Desde la superficie positiva (x=0.04) hasta la negativa (x=0.07)
- El campo es el de una carga puntual situada en el centro de la esfera positiva
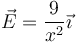
- siendo el trabajo
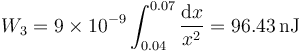
- Desde la superficie negativa (x=0.07) hasta D (x=0.08)
- Aquí el campo es suma del de dos cargas
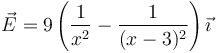
- siendo el trabajo
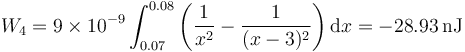
Sumando las cuatro contribuciones
W = 45+ 96.43 -28.93 = 112.5\mathrm{nJ}\mathrm{nJ}





