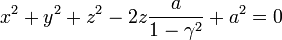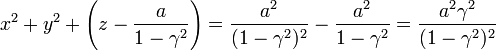Potencial de dos cargas puntuales
De Laplace
(→Solución) |
(→Solución) |
||
| Línea 5: | Línea 5: | ||
El potencial creado por estas dos cargas en cualquier punto del espacio es | El potencial creado por estas dos cargas en cualquier punto del espacio es | ||
| - | <center><math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{ | + | <center><math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{|\mathbf{r}-\mathbf{r}_1|}-\frac{q_2}{|\mathbf{r}-\mathbf{r}_2|}\right)</math></center> |
| + | |||
| + | La equipotencial V=0 vendrá dada por la ecuación | ||
| + | |||
| + | <center><math>\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{|\mathbf{r}-\mathbf{r}_1|}-\frac{q_2}{|\mathbf{r}-\mathbf{r}_2|}\right)=0</math></center> | ||
| + | |||
| + | No es evidente que ésta sea la ecuación de una esfera. Para ponerlo de manifiesto reescribimos la ecuación como | ||
| + | |||
| + | <center><math>\left|\mathbf{r}-\mathbf{r}_2|=\gamma \left|\mathbf{r}-\mathbf{r}_1|</math>{{qquad}}<math>\gamma=\frac{q_2}{q_1}</math></center> | ||
| + | |||
| + | Podemos tomar el origen de coordenadas en la carga <math>q_1</math> y el eje Z el que pasa por las dos cargas, de forma que <math>\mathbf{r}_2=a\mathbf{u}_z</math>. Expresando el vector de posición en cartesianas esta ecuación queda | ||
| + | |||
| + | <center><math>\sqrt{x^2+y^2+(z-a)^2}=\gamma \sqrt{x^2+y^2+z^2}</math></center> | ||
| + | |||
| + | Elevando al cuadrado y agrupando términos | ||
| + | |||
| + | <center><math>\left(x^2+y^2+z^2\right)\left(1-\gamma^2\right)-2za + a^2 = 0</math></center> | ||
| + | |||
| + | Esta es ya claramente la ecuación de una esfera. Para identificar su radio y la posición del centro, despejamos y competamos cuadrados | ||
| + | |||
| + | <center><math>x^2+y^2+z^2-2z\frac{a}{1-\gamma^2} + a^2 = 0</math></center> | ||
| + | |||
| + | <center><math>x^2+y^2+\left(z-\frac{a}{1-\gamma^2}\right) = \frac{a^2}{(1-\gamma^2)^2}-\frac{a^2}{1-\gamma^2}=\frac{a^2\gamma^2}{(1-\gamma^2)^2}</math></center> | ||
| + | |||
| + | |||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 13:50 1 nov 2009
1 Enunciado
Halle el potencial creado por dos cargas q1, − q2 situadas a una distancia a una de la otra. Demuestre que la superficie equipotencial V = 0 es una esfera.
2 Solución
El potencial creado por estas dos cargas en cualquier punto del espacio es
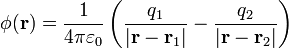
La equipotencial V=0 vendrá dada por la ecuación
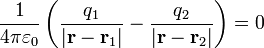
No es evidente que ésta sea la ecuación de una esfera. Para ponerlo de manifiesto reescribimos la ecuación como
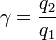
Podemos tomar el origen de coordenadas en la carga q1 y el eje Z el que pasa por las dos cargas, de forma que 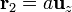 . Expresando el vector de posición en cartesianas esta ecuación queda
. Expresando el vector de posición en cartesianas esta ecuación queda
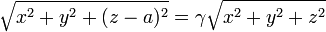
Elevando al cuadrado y agrupando términos

Esta es ya claramente la ecuación de una esfera. Para identificar su radio y la posición del centro, despejamos y competamos cuadrados