Problemas de corriente eléctrica (GIA)

De Laplace

Revisión de 12:54 5 abr 2013 (ver código fuente) Gabriel (Discusión | contribuciones) ← Edición más antigua		Revisión de 13:01 5 abr 2013 (ver código fuente) Gabriel (Discusión | contribuciones) (→Asociación de resistencias independiente de la temperatura) Edición más nueva →
Línea 10:		Línea 10:
	'''Datos''': <math>\rho_\mathrm{Cu}^0=1.7\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}\,</math> <math>\rho_\mathrm{C}^0=3500\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}</math> <math>\alpha_\mathrm{Cu}=3.9\times10^{-3}\,\mbox{K}^{-1}\,\mathrm{;}\,</math> <math>\alpha_\mathrm{C}=-0.5\times10^{-3}\,\mbox{K}^{-1}</math>.		'''Datos''': <math>\rho_\mathrm{Cu}^0=1.7\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}\,</math> <math>\rho_\mathrm{C}^0=3500\times10^{-8}\,\Omega\,\mathrm{m}\,\mathrm{;}</math> <math>\alpha_\mathrm{Cu}=3.9\times10^{-3}\,\mbox{K}^{-1}\,\mathrm{;}\,</math> <math>\alpha_\mathrm{C}=-0.5\times10^{-3}\,\mbox{K}^{-1}</math>.
		+
		+
		+	<center>[[Archivo:resit_no_temp_0.gif]]</center>
	==[[Conexiones serie y paralelo de bombillas a batería real GIA|Conexiones serie y paralelo de bombillas a una batería]]==		==[[Conexiones serie y paralelo de bombillas a batería real GIA|Conexiones serie y paralelo de bombillas a una batería]]==

---

Revisión de 13:01 5 abr 2013

Contenido 1 Proceso de carga de una esfera conductora 2 Asociación de resistencias independiente de la temperatura 3 Conexiones serie y paralelo de bombillas a una batería

1 Proceso de carga de una esfera conductora

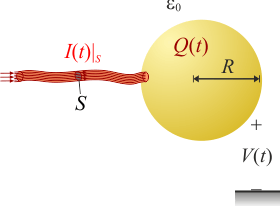
A una esfera metálica de radio R, inicialmente descargada, llega una corriente eléctrica a través de un delgado hilo conductor. La intensidad de la corriente decae exponencialmente en el tiempo según la ley I(t) = I₀e ^{− t / τ}, donde I₀ es la intensidad de corriente inicial y τ es un valor constante con dimensiones de tiempo (constante de relajación). ¿Cómo será el valor del potencial electrostático en la esfera al cabo de un tiempo suficientemente grande ()?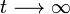

2 Asociación de resistencias independiente de la temperatura

Un cable de cobre de sección transversal A y longitud l_Cu se conecta en serie con un cable de carbono de la misma sección transversal y longitud l_C. Halle la relación de las longitudes de ambos cables para que la resistencia total del dispositivo sea independiente de la temperatura. Explicar por qué esta relación sólo asegura independencia de la resistencia con la R con la temperatura para pequeñas variaciones de dicha magnitud.

Datos: .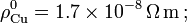

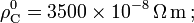
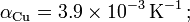
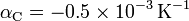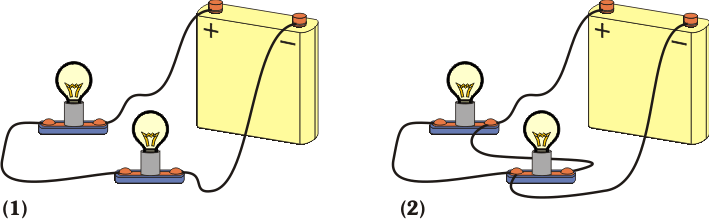
3 Conexiones serie y paralelo de bombillas a una batería

Se dispone de una batería de 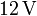con una resistencia interna de 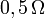y de dos pequeñas bombillas iguales. Cada bombilla puede modelarse como una resistencia de .

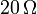1. Si se conectan ambas bombillas en serie a la batería, ¿cuál de ellas dará más luz?
2. Si a continuación se conectan en paralelo, ¿iluminarán más o menos?