Frenado de un fórmula 1
De Laplace
(→Aceleración en el SI) |
|||
| Línea 23: | Línea 23: | ||
Si contamos como instante inicial el del comienzo de la frenada, ya tenemos <math>x_0</math> y <math>v_0</math>. Para el final de la frenada nos queda | Si contamos como instante inicial el del comienzo de la frenada, ya tenemos <math>x_0</math> y <math>v_0</math>. Para el final de la frenada nos queda | ||
| - | x_2 = x_1 + v_1 t + \frac{1}{2}at^2 \qquad v_2 = v_1 + a t | + | <center><math>x_2 = x_1 + v_1 t + \frac{1}{2}at^2 \qquad v_2 = v_1 + a t</math></center> |
| + | |||
| + | Elevando la segunda ecuación al cuadrado podemos eliminar el tiempo | ||
| + | |||
| + | <center><math>v_2^2 = v_1^2 + 2av_1 t + a^2 t^2 = v_1^2 + 2a\left(v_1t + \frac{1}{2}at^2\right) = v_1^2 + 2a(x_2-x_1)</math></center> | ||
| + | |||
| + | Despejando | ||
| + | |||
| + | <center><math>a = \frac{v_2^2 - v_1^2}{2(x_2-x_1)}</math></center> | ||
| + | |||
| + | Este resultado es un caso particular de la fórmula general | ||
| + | |||
| + | <center><math>a = \frac{\mathrm{d}\ }{\mathrm{d}x}\left(\frac{1}{2}v^2\right)</math></center> | ||
| + | |||
| + | que cuando la aceleración es constante se reduce a un cociente entre incrementos. | ||
| + | |||
| + | Sustituyendo los valores numéricos nos queda | ||
| + | |||
| + | <center><math>a = \frac{(22.2\mathrm{m}/\mathrm{s})^2-(94.4\mathrm{m}/\mathrm{s})^2}{2(0\,\mathrm{m}-(-150\,\mathrm{m})} = -28.1\frac{\mathrm{m}}{\mathrm{s}^2}</math></center> | ||
==“Fuerzas G”== | ==“Fuerzas G”== | ||
==Velocidad como función de la posición== | ==Velocidad como función de la posición== | ||
[[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | [[Categoría:Problemas de cinemática del movimiento rectilíneo (GIE)]] | ||
Revisión de 16:32 16 oct 2012
Contenido |
1 Enunciado
Cuando el Ferrari de Fernando Alonso se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 340 km/h. Cuando entra en la chicane va a 80 km/h.
- Suponiendo que la aceleración es constante, determine su valor.
- Exprese el resultado en el SI y como un múltiplo de g (siendo
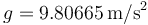 ).
).
- Determine la velocidad como función de la posición y represéntela gráficamente.
2 Aceleración en el SI
Pasamos en primer lugar los valores de la velocidad al SI. A 150m de la chicane tiene una velocidad de
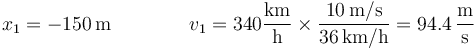
y al entrar en la chicane
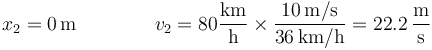
Para hallar la aceleración aplicamos que en un movimiento uniformemente acelerado

En este caso no conocemos lo que tarda en llegar a la chicane, pero no es necesario. tenemos dos ecuaciones y dos incógnitas (la aceleración y el intervalo de frenado).
Si contamos como instante inicial el del comienzo de la frenada, ya tenemos x0 y v0. Para el final de la frenada nos queda

Elevando la segunda ecuación al cuadrado podemos eliminar el tiempo

Despejando

Este resultado es un caso particular de la fórmula general

que cuando la aceleración es constante se reduce a un cociente entre incrementos.
Sustituyendo los valores numéricos nos queda






