Problemas de vectores libres (G.I.T.I.)
De Laplace
(→Seno y coseno de una diferencia) |
|||
| Línea 17: | Línea 17: | ||
:(h) <math>\frac{W}{t} = \vec{F}\times\left(\vec{v}-\frac{R}{t}\right)</math> | :(h) <math>\frac{W}{t} = \vec{F}\times\left(\vec{v}-\frac{R}{t}\right)</math> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==[[Paralelogramo en cuadrilátero]]== | ==[[Paralelogramo en cuadrilátero]]== | ||
Sea ABCD un cuadrilátero arbitrario. Demuestre, usando el álgebra vectorial, que los puntos medios de sus cuatro lados constituyen los vértices de un paralelogramo. | Sea ABCD un cuadrilátero arbitrario. Demuestre, usando el álgebra vectorial, que los puntos medios de sus cuatro lados constituyen los vértices de un paralelogramo. | ||
| - | ==[[ | + | ==[[Lados de un triángulo rectángulo (Ex.Nov/11)]]== |
| - | + | ¿Cuál de las siguientes ternas de vectores libres podría corresponder a los tres lados de un triángulo rectángulo? | |
| - | + | 1) <math>\,\,\,\vec{a}=(-\vec{\imath}+4\,\vec{\jmath}+\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, | |
| + | \vec{b}=(2\,\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, | ||
| + | \vec{c}=(-\vec{\imath}-5\,\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m}\,</math> | ||
| - | == | + | 2) <math>\,\,\,\vec{a}=(3\,\vec{\imath}+2\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, |
| - | + | \vec{b}=(2\,\vec{\imath}-3\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, | |
| + | \vec{c}=(5\,\vec{\imath}+\vec{k}\,)\,\mathrm{m}\,</math> | ||
| - | == | + | 3) <math>\,\,\,\vec{a}=(\vec{\imath}-2\,\vec{\jmath}+3\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, |
| + | \vec{b}=(-2\,\vec{\imath}+3\,\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, | ||
| + | \vec{c}=(-\vec{\imath}+\vec{\jmath}+\vec{k}\,)\,\mathrm{m}\,</math> | ||
| - | + | 4) <math>\,\,\,\vec{a}=(3\,\vec{\jmath}+3\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, | |
| + | \vec{b}=(\vec{\imath}+2\,\vec{\jmath}+2\,\vec{k}\,)\,\mathrm{m;}\,\,\,\,\, | ||
| + | \vec{c}=(2\,\vec{\imath}+\vec{\jmath}-2\,\vec{k}\,)\,\mathrm{m}\,</math> | ||
| - | A | + | ==[[Arco capaz]]== |
| + | Sean <math>A</math> y <math>B</math> dos puntos diametralmente opuestos en una circunferencia c. Sea <math>P</math> otro punto de la misma circunferencia. Demuestre que los vectores <math>\overrightarrow{AP}</math> y <math>\overrightarrow{BP}</math> son ortogonales. | ||
| - | < | + | Inversamente, sean <math>A</math>, <math>B</math> y <math>P</math> tres puntos tales que <math>\overrightarrow{AP} \perp \overrightarrow{BP}</math>. Sea <math>C</math> el punto medio entre <math>A</math> y <math>B</math>. Pruebe que <math>|\overrightarrow{CP}| = |\overrightarrow{CA}|</math>. |
| - | + | ==[[Ejemplo de ecuación vectorial de un plano]]== | |
| + | Obtenga la ecuación del plano perpendicular al vector libre <math>\vec{a}= 2\vec{\imath}+3\vec{\jmath}+6\vec{k}</math> y que contiene a un punto <math>P</math>, cuya posición respecto del origen de un sistema de referencia <math>OXYZ</math> viene dada por el radiovector <math>\vec{r} = \vec{\imath} + 5\vec{\jmath} + 3\vec{k}</math>. Calcule la distancia que separa a dicho plano del origen <math>O</math>. (Unidades del SI) | ||
==[[Teoremas del seno y del coseno]]== | ==[[Teoremas del seno y del coseno]]== | ||
| Línea 64: | Línea 62: | ||
en un triángulo de lados <math>a</math>, <math>b</math> y <math>c</math>, y ángulos opuestos <math>\alpha</math>, <math>\beta</math> y <math>\gamma</math>. | en un triángulo de lados <math>a</math>, <math>b</math> y <math>c</math>, y ángulos opuestos <math>\alpha</math>, <math>\beta</math> y <math>\gamma</math>. | ||
| - | ==[[ | + | ==[[Seno y coseno de una diferencia]]== |
| - | + | ||
| - | + | [[Archivo:diferencia-angulos.png|left]] | |
| - | + | A partir del producto escalar y del producto vectorial de dos vectores unitarios en un plano, demuestre las fórmulas trigonométricas para el coseno y el seno de la diferencia de dos ángulos: | |
| - | + | <center><math>\cos(\beta-\alpha) = \cos(\alpha)\cos(\beta)+\,\mathrm{sen}\,(\alpha)\,\mathrm{sen}\,(\beta)</math></center> | |
| - | + | ||
| - | + | <center><math>\mathrm{sen}\,(\beta-\alpha) = \cos(\alpha)\,\mathrm{sen}\,(\beta)-\,\mathrm{sen}\,(\alpha)\cos(\beta)</math></center> | |
| - | + | ||
| - | ==[[Ejemplo de | + | ==[[Ejemplo de clasificación de vectores]]== |
| - | + | De los siguientes vectores ligados con sus respectivos puntos de aplicación: | |
| - | < | + | :a) <math>\vec{v}_1 = 2\vec{\imath}-\vec{\jmath} + \vec{k}</math> en <math>A(3,1,1)\,</math> |
| + | :b) <math>\vec{v}_2 = 2\vec{\imath}+\vec{\jmath} + \vec{k}</math> en <math>B(1,2,0)\,</math> | ||
| + | :c) <math>\vec{v}_3 = 2\vec{\imath}-\vec{\jmath} + \vec{k}</math> en <math>C(-1,3,-1)\,</math> | ||
| + | :d) <math>\vec{v}_4 = 2\vec{\imath}-\vec{\jmath} + \vec{k}</math> en <math>D(-3,4,-1)\,</math> | ||
| + | :e) <math>\vec{v}_5 = 2\vec{\imath}+\vec{\jmath} + \vec{k}</math> en <math>E(7,5,3)\,</math> | ||
| - | + | indique cuáles pueden representar al mismo vector deslizante y cuáles al mismo vector libre. | |
| - | + | ==[[Longitud de una sombra (Ex.Nov/11)]]== | |
| - | + | En cierto sistema de coordenadas cartesianas, el suelo viene definido por el plano de ecuación <math>x-2y+2z=0\,</math> y en él se halla clavada una varilla rectilínea representada por el vector <math>\overrightarrow{OP}=(4\,\vec{\imath}-3\,\vec{\jmath}\,)\,\mathrm{m}</math>. Suponiendo que es mediodía y los rayos solares inciden | |
| - | + | perpendicularmente al suelo, ¿cuál es la longitud de la sombra que la varilla proyecta sobre el suelo? | |
| - | + | ==[[Volumen de un paralelepípedo]]== | |
| - | ==[[ | + | Sean los puntos de coordenadas (en el SI) <math>O(1,0,2)</math>, <math>A(3,2,4)</math>, <math>B(2,6,8)</math> y <math>C(2,-3,1)</math>. Determine el volumen del paralelepípedo definido por los vectores <math>\overrightarrow{OA}</math>, <math>\overrightarrow{OB}</math> y <math>\overrightarrow{OC}</math>. |
| - | + | ||
| - | + | Halle del mismo modo el volumen del paralelepípedo definido por los vectores <math>\overrightarrow{AO}</math>, <math>\overrightarrow{AB}</math> y <math>\overrightarrow{AC}</math>. | |
| - | + | Calcule igualmente el volumen del tetraedro irregular definido por estos cuatro puntos. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==[[Vectores con tres condiciones (Ex.Nov/11)]]== | ==[[Vectores con tres condiciones (Ex.Nov/11)]]== | ||
| Línea 134: | Línea 104: | ||
<math>\,\vec{k}\,</math> m un paralelepípedo de volumen igual a <math>6</math> m<math>^{3}</math>. | <math>\,\vec{k}\,</math> m un paralelepípedo de volumen igual a <math>6</math> m<math>^{3}</math>. | ||
| - | ==[[ | + | ==[[Ejemplo de construcción de una base]]== |
| - | + | Dados los vectores | |
| - | + | <center><math>\vec{v}=\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{a}=6\vec{\imath}+9\vec{\jmath}+6\vec{k}</math></center> | |
| - | + | ||
| - | \vec{ | + | |
| - | + | Construya una base ortonormal dextrógira cuyos vectores cumplan las siguientes condiciones: | |
| - | + | ||
| - | + | ||
| - | + | * El primer vector tiene la dirección y sentido de <math>\vec{v}</math> | |
| - | \vec{ | + | * El segundo vector está contenido en el plano definido por <math>\vec{v}</math> y <math>\vec{a}</math>, y apunta hacia el mismo semiplano (respecto de <math>\vec{v}</math>) que el vector <math>\vec{a}</math>. |
| - | + | * El tercer vector es perpendicular a los dos anteriores, y está orientado según la regla de la mano derecha. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==[[Calcular el ángulo entre dos vectores]]== | ==[[Calcular el ángulo entre dos vectores]]== | ||
| Línea 183: | Línea 141: | ||
Si a esta fuerza se le suma otra <math>\vec{F}_2 = (-10\vec{\imath}-10\vec{\jmath})\,\mathrm{N}</math>, ¿qué ángulo forma la resultante con los ejes coordenados? | Si a esta fuerza se le suma otra <math>\vec{F}_2 = (-10\vec{\imath}-10\vec{\jmath})\,\mathrm{N}</math>, ¿qué ángulo forma la resultante con los ejes coordenados? | ||
| + | |||
| + | ==[[Diagonales de un rombo]]== | ||
| + | Demuestre que las diagonales de un rombo son perpendiculares entre sí. | ||
| + | |||
| + | ==[[Cálculo de distancia entre dos rectas]]== | ||
| + | Sean las rectas <math>r_1</math>, que pasa por los puntos <math>A(-2,5,1)</math> y <math>B(7,-7,1)</math>, y <math>r_2</math> que pasa por <math>C(5,4,-3)</math> y <math>D(5,4,2)</math> (todas las unidades en el SI). Empleando el álgebra vectorial, determine la distancia entre estas dos rectas. | ||
| + | |||
| + | ==[[Sistema de ecuaciones vectoriales]]== | ||
| + | Demuestre que si se cumplen simultáneamente las condiciones | ||
| + | |||
| + | <center><math>\vec{A}\cdot\vec{B} = \vec{A}\cdot\vec{C}</math>{{qquad}}{{qquad}}<math>\vec{A}\times\vec{B} = \vec{A}\times\vec{C}</math></center> | ||
| + | |||
| + | siendo <math>\vec{A}\neq \vec{0}</math>, entonces <math>\vec{B} = \vec{C}</math>; pero si se cumple una de ellas y la otra no, entonces <math>\vec{B}\neq\vec{C}</math>. | ||
| + | |||
| + | <!-- | ||
| + | ==[[Cálculo de base dual]]== | ||
| + | Sea <math>B_1=\{\vec{v}_1,\vec{v}_2,\vec{v}_3\}</math> una base vectorial arbitraria. Sean <math>\{\vec{w}_1,\vec{w}_2,\vec{w}_3\}</math> tres vectores definidos por | ||
| + | |||
| + | <center><math>\vec{w}_1=\frac{\vec{v}_2\times\vec{v}_3}{\Delta}</math>{{qquad}}{{qquad}}<math>\vec{w}_2=\frac{\vec{v}_3\times\vec{v}_1}{\Delta}</math>{{qquad}}{{qquad}}<math>\vec{w}_3=\frac{\vec{v}_1\times\vec{v}_2}{\Delta}</math>{{qquad}}{{qquad}}<math>\Delta =\vec{v}_1\cdot(\vec{v}_2\times\vec{v}_3)</math></center> | ||
| + | |||
| + | : 1. Demuestre que el conjunto <math>B_2=\{\vec{w}_1,\vec{w}_2,\vec{w}_3\}</math> es también una base (llamada ''base dual'' de <math>B_1</math>). ¿Cuánto vale el producto mixto de sus vectores? | ||
| + | : 2. Pruebe que se cumple | ||
| + | |||
| + | <center><math>\vec{v}_i\cdot\vec{w}_k=\begin{cases} 1 & i = k \\ 0 & i\neq 0\end{cases}</math></center> | ||
| + | |||
| + | : 3. Demuestre que las componentes de un vector en la base <math>B_1</math> pueden calcularse proyectando sobre la base <math>B_2</math>, esto es, si | ||
| + | |||
| + | <center><math>\vec{F} = F_1\vec{v}_1 + F_2\vec{v}_2 + F_3\vec{v}_3</math></center> | ||
| + | |||
| + | : la componente k viene dada por | ||
| + | |||
| + | <center><math>F_k = \vec{F}\cdot\vec{w}_k</math></center> | ||
| + | |||
| + | : 4. Halle la base dual de la base | ||
| + | |||
| + | <center><math>B_1 =\{\vec{\imath},\vec{\imath}+\vec{\jmath},\vec{\imath}+\vec{\jmath}+\vec{k}\}</math></center> | ||
| + | |||
| + | : 5. Calcule las componentes del vector | ||
| + | |||
| + | <center><math>\vec{F} = 2\vec{\imath}-3\vec{\jmath}+\vec{k}</math></center> | ||
| + | |||
| + | : en las bases del apartado anterior. | ||
| + | --> | ||
[[Categoría:Problemas de vectores libres (G.I.T.I.)|0]] | [[Categoría:Problemas de vectores libres (G.I.T.I.)|0]] | ||
Revisión de 17:53 19 sep 2012
1 Formulas potencialmente incorrectas
De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de ejemplos de análisis dimensional, R es una distancia y  el vector de posición; t es el tiempo:
el vector de posición; t es el tiempo:
- (a)
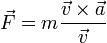
- (b)
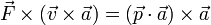
- (c)
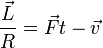
- (d)
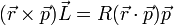
- (e)
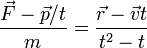
- (f)
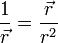
- (g)
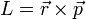
- (h)
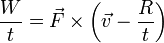
2 Paralelogramo en cuadrilátero
Sea ABCD un cuadrilátero arbitrario. Demuestre, usando el álgebra vectorial, que los puntos medios de sus cuatro lados constituyen los vértices de un paralelogramo.
3 Lados de un triángulo rectángulo (Ex.Nov/11)
¿Cuál de las siguientes ternas de vectores libres podría corresponder a los tres lados de un triángulo rectángulo?
1) 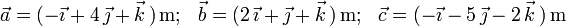
2) 
3) 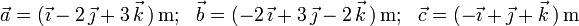
4) 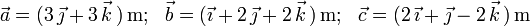
4 Arco capaz
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores 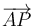 y
y 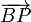 son ortogonales.
son ortogonales.
Inversamente, sean A, B y P tres puntos tales que 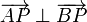 . Sea C el punto medio entre A y B. Pruebe que
. Sea C el punto medio entre A y B. Pruebe que 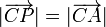 .
.
5 Ejemplo de ecuación vectorial de un plano
Obtenga la ecuación del plano perpendicular al vector libre 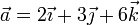 y que contiene a un punto P, cuya posición respecto del origen de un sistema de referencia OXYZ viene dada por el radiovector
y que contiene a un punto P, cuya posición respecto del origen de un sistema de referencia OXYZ viene dada por el radiovector 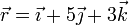 . Calcule la distancia que separa a dicho plano del origen O. (Unidades del SI)
. Calcule la distancia que separa a dicho plano del origen O. (Unidades del SI)
6 Teoremas del seno y del coseno
Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno
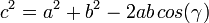
y del seno
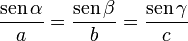
en un triángulo de lados a, b y c, y ángulos opuestos α, β y γ.
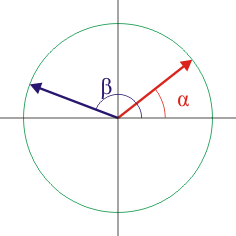
7 Seno y coseno de una diferencia
A partir del producto escalar y del producto vectorial de dos vectores unitarios en un plano, demuestre las fórmulas trigonométricas para el coseno y el seno de la diferencia de dos ángulos:


8 Ejemplo de clasificación de vectores
De los siguientes vectores ligados con sus respectivos puntos de aplicación:
- a)
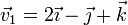 en
en 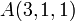
- b)
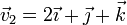 en
en 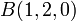
- c)
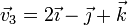 en
en 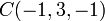
- d)
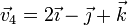 en
en 
- e)
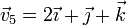 en
en 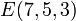
indique cuáles pueden representar al mismo vector deslizante y cuáles al mismo vector libre.
9 Longitud de una sombra (Ex.Nov/11)
En cierto sistema de coordenadas cartesianas, el suelo viene definido por el plano de ecuación 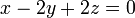 y en él se halla clavada una varilla rectilínea representada por el vector
y en él se halla clavada una varilla rectilínea representada por el vector 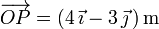 . Suponiendo que es mediodía y los rayos solares inciden
perpendicularmente al suelo, ¿cuál es la longitud de la sombra que la varilla proyecta sobre el suelo?
. Suponiendo que es mediodía y los rayos solares inciden
perpendicularmente al suelo, ¿cuál es la longitud de la sombra que la varilla proyecta sobre el suelo?
10 Volumen de un paralelepípedo
Sean los puntos de coordenadas (en el SI) O(1,0,2), A(3,2,4), B(2,6,8) y C(2, − 3,1). Determine el volumen del paralelepípedo definido por los vectores  ,
, 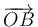 y
y  .
.
Halle del mismo modo el volumen del paralelepípedo definido por los vectores  ,
, 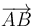 y
y 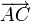 .
.
Calcule igualmente el volumen del tetraedro irregular definido por estos cuatro puntos.
11 Vectores con tres condiciones (Ex.Nov/11)
Determine todos los vectores libres que cumplen simultáneamente las tres siguientes condiciones:
1) Tener una longitud de 14 m.
2) Ser ortogonal al vector 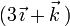 m.
m.
3) Formar junto a los vectores 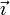 m y
m y
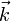 m un paralelepípedo de volumen igual a 6 m3.
m un paralelepípedo de volumen igual a 6 m3.
12 Ejemplo de construcción de una base
Dados los vectores
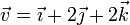
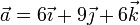
Construya una base ortonormal dextrógira cuyos vectores cumplan las siguientes condiciones:
- El primer vector tiene la dirección y sentido de

- El segundo vector está contenido en el plano definido por
 y
y  , y apunta hacia el mismo semiplano (respecto de
, y apunta hacia el mismo semiplano (respecto de  ) que el vector
) que el vector  .
.
- El tercer vector es perpendicular a los dos anteriores, y está orientado según la regla de la mano derecha.
13 Calcular el ángulo entre dos vectores
Halle el ángulo que forman los vectores
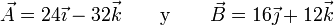
14 Ejemplo de operaciones con dos vectores
Dados los vectores

- ¿Qué ángulo forman estos dos vectores?
- ¿Qué área tiene el paralelogramo que tiene a estos dos vectores por lados?
- Escriba
 como suma de dos vectores, uno paralelo a
como suma de dos vectores, uno paralelo a  y otro ortogonal a él.
y otro ortogonal a él.
15 Determinación de un vector a partir de sus proyecciones
Se tiene un vector conocido, no nulo,  y uno que se desea determinar,
y uno que se desea determinar, 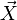 . Se dan como datos su producto escalar y su
producto vectorial por
. Se dan como datos su producto escalar y su
producto vectorial por 

Determine el valor de 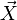 . ¿Es suficiente una sola de las dos ecuaciones para hallar
. ¿Es suficiente una sola de las dos ecuaciones para hallar 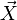 ?
?
16 Cálculo de las componentes de un vector
De una fuerza 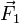 se sabe que tiene de intensidad 10 N y que los ángulos que forma con los semiejes OX y OY positivos valen 60°. Determine las componentes cartesianas de esta fuerza. ¿Existe solución? ¿Es única?
se sabe que tiene de intensidad 10 N y que los ángulos que forma con los semiejes OX y OY positivos valen 60°. Determine las componentes cartesianas de esta fuerza. ¿Existe solución? ¿Es única?
Si a esta fuerza se le suma otra 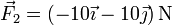 , ¿qué ángulo forma la resultante con los ejes coordenados?
, ¿qué ángulo forma la resultante con los ejes coordenados?
17 Diagonales de un rombo
Demuestre que las diagonales de un rombo son perpendiculares entre sí.
18 Cálculo de distancia entre dos rectas
Sean las rectas r1, que pasa por los puntos A( − 2,5,1) y B(7, − 7,1), y r2 que pasa por C(5,4, − 3) y D(5,4,2) (todas las unidades en el SI). Empleando el álgebra vectorial, determine la distancia entre estas dos rectas.
19 Sistema de ecuaciones vectoriales
Demuestre que si se cumplen simultáneamente las condiciones
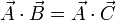
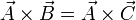
siendo 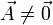 , entonces
, entonces 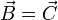 ; pero si se cumple una de ellas y la otra no, entonces
; pero si se cumple una de ellas y la otra no, entonces 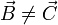 .
.