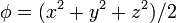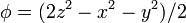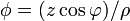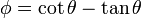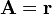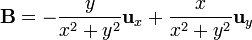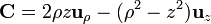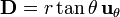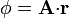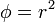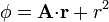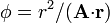Problemas de fundamentos matemáticos
De Laplace
(Diferencias entre revisiones)
| Línea 14: | Línea 14: | ||
# <math>\mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}</math> | # <math>\mathbf{C} = 2\rho z\mathbf{u}_{\rho}-(\rho^2-z^2)\mathbf{u}_{z}</math> | ||
# <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math> | # <math>\mathbf{D}=r\tan\theta\,\mathbf{u}_{\theta}</math> | ||
| + | |||
| + | ==Trazado de superficies equiescalares== | ||
| + | Describa las superficies equipotenciales de los siguientes campos escalares | ||
| + | |||
| + | # <math>\phi=\mathbf{A}{\cdot}\mathbf{r}\,</math> | ||
| + | # <math>\phi=r^2\,</math> | ||
| + | # <math>\phi=\mathbf{A}{\cdot}\mathbf{r}+r^2\,</math> | ||
| + | # <math>\phi= r^2/(\mathbf{A}{\cdot}\mathbf{r})</math> | ||
| + | |||
| + | donde <math>\mathbf{A}</math> es un vector constante y <math>\mathbf{r}</math> es el vector de posición. | ||
[[Categoría:Problemas de fundamentos matemáticos]] | [[Categoría:Problemas de fundamentos matemáticos]] | ||
Revisión de 08:40 23 sep 2008
1 Campos escalares en diferentes sistemas
Exprese los siguientes campos escalares en coordenadas cartesianas, cilíndricas y esféricas
2 Campos vectoriales en diferentes sistemas
Exprese los siguientes campos vectoriales en coordenadas cartesianas, cilíndricas y esféricas:
3 Trazado de superficies equiescalares
Describa las superficies equipotenciales de los siguientes campos escalares
donde 
es un vector constante y 
es el vector de posición.
