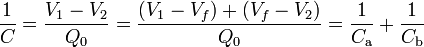Condensador plano de capacidad ajustable GIA
De Laplace
(→Capacidad con la lámina de dieléctrico) |
(→Capacidad con la lámina de dieléctrico) |
||
| Línea 42: | Línea 42: | ||
Las capacidades de los condensadores de la asociación son: | Las capacidades de los condensadores de la asociación son: | ||
| - | <center><math>C_\mathrm{a}=\frac{Q_0}{V_1-V_f}\simeq\kappa\ \frac{\varepsilon_0\!\ S}{d}\,\mathrm{;}\quad C_\mathrm{b}=\frac{Q_0}{V_f-V_2}\simeq \frac{\varepsilon_0\!\ S}{a-d}</math></center> | + | <center><math>C_\mathrm{a}=\frac{Q_0}{V_1-V_f}\simeq\kappa\ \frac{\varepsilon_0\!\ S}{d}\approx 17.7\,\mathrm{pF}\,\mathrm{;}\quad C_\mathrm{b}=\frac{Q_0}{V_f-V_2}\simeq \frac{\varepsilon_0\!\ S}{a-d}\approx 2.21\,\mathrm{pF}</math></center> |
| + | |||
| + | Para obtener el valor de la capacidad equivalente <math>C</math> aplicamos que la carga almacenada en cada uno de los de la asociación en serie es la misma que en el equivalente. Y la diferencia de potencial en éste debe ser la suma de las diferencias de potencial en los de la asociación. Es decir, | ||
| + | |||
| + | <center><math>\frac{1}{C}=\frac{V_1-V_2}{Q_0}=\frac{(V_1-V_f)+(V_f-V_2)}{Q_0}=\frac{1}{C_\mathrm{a}}+\frac{1}{C_\mathrm{b}}</math></center> | ||
| - | |||
[[Categoría:Problemas de capacidad eléctrica F2 GIA]] | [[Categoría:Problemas de capacidad eléctrica F2 GIA]] | ||
Revisión de 18:08 31 mar 2012
Contenido |
1 Enunciado
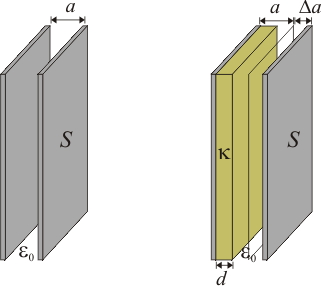
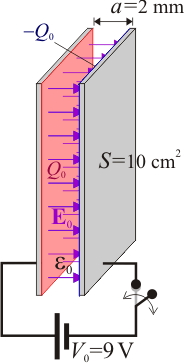
Las armaduras de un condensador plano tienen una superficie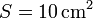 y están separadas una distancia
y están separadas una distancia 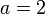 mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A continuación se coloca una placa de material dieléctrico de espesor
mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A continuación se coloca una placa de material dieléctrico de espesor 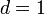 mm y de constante dieléctrica κ = 2 pegada a una de sus armaduras. Calcular:
mm y de constante dieléctrica κ = 2 pegada a una de sus armaduras. Calcular:
- Carga eléctrica en cada armadura del condensador.
- Capacidad del condensador con el dieléctrico.
- Distancia adicional que deben separarse las armaduras del condensador después de introducir el dieléctrico para que su capacidad sea la misma que tenía antes de introducir el dieléctrico.
- Energía electrostática almacenada en el condensador relleno de aire, con la placa dieléctrica y después de separar las armaduras.
2 Solución
En el sistema de conductores planos descrito, la distancia a de separación entre las placas es considerablemente menor que las dimensiones de los conductores. Considerando que éstos fueran aproximadamente cuadrados, y con los valores indicados en el enunciado, se tendría que la relación entre las longitudes de los lados de las armaduras metálicas y la distancia que las separa es del orden de...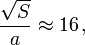
suficiente para considerar en primera aproximación que, una vez cargados los planos conductures y alejados de otras distrubciondes de carga, aquéllos se van a encontrar en influencia total. Es decir, todas las líneas del campo eléctrico que salen de una placa terminan en la otra, de manera que ambas van a almacenar cantidades opuestas de carga, Q y − Q. Además, podemos considerar que la carga eléctrica se distribuirá casi uniformemente en cada una de las superficies interiores (enfrentadas) de las placas conductoras, pudiendo despreciarse los efectos de acumulación de carga eléctrica en los bordes. Es decir, el sistema bajo estudio se aproxima bastante al modelo ideal de condensador plano paralelo, cuya capacidad eléctrica (es decir, la relación entre la carga en uno de los conductores y al diferencia de potencial entre ambos), es
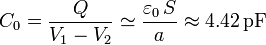
cuando las placas o armaduras conducturas de sección S están separadas por una distancia a vacía (ausente de cualquier medio material).
2.1 Carga eléctrica en las armaduras
Si las placas se conectan a una batería que establece un valor fijo de diferencia de potencial entre ellas, almacenarán cantidades opuestas de carga eléctrica,
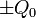 :
:
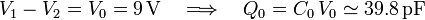
Una vez cargado el condensador, se desconecta la batería. Al quedar las placas aisladas, éstas mantendrán las cantidades de carga 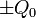 . Y como la capacidad eléctrica es un factor que depende de la geometría del sistema y ésta no ha cambiado, la diferencia de potencial entre los conductores seguirá siendo de 9 V, a pesar de que ya no están conectados a los bornes de la batería.
. Y como la capacidad eléctrica es un factor que depende de la geometría del sistema y ésta no ha cambiado, la diferencia de potencial entre los conductores seguirá siendo de 9 V, a pesar de que ya no están conectados a los bornes de la batería.
2.2 Capacidad con la lámina de dieléctrico
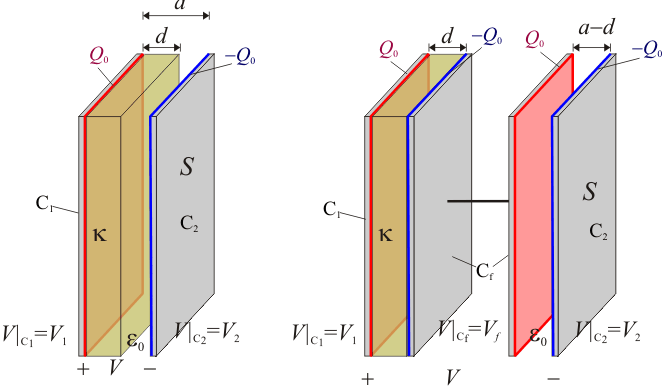
Si un condensador se rellena con un medio dieléctrico lineal, la capacidad aumenta en un factor κ denominado constante dieléctrica del material. Además, cambia la geometría del sistema al reducirse el espesor de la región vacía al valor a − d. Por tanto, la introducción de la lámina dieléctrica de espesor d hará cambiar la capacidad del sistema bajo estudio, aunque no rellene completamente el espacio entre las placas conductoras. En consecuencia, cambia la relación entre carga almacenada en los conductores y diferencia de potencial entre ellos. Y si la carga no puede cambiar por estar los conductores aislados (desconectados), debe hacerlo la diferencia de potencial entre las placas, si bien, se seguirá cumpliendo que éstas deben ser superficies equipotenciales.
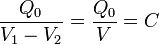
Como la distancia entre las placas sigue siendo pequeña frente a sus dimensiones podemos asegurar que el campo eléctrico mantiene su dirección perpendicular a los planos conductores en toda la región comprendida entre ellos. En consecuencia, las superficies equipotenciales serán planos paralelos a los conductores. Fijémonos en la superficie equipotencial que coincide con la interfaz (superficie de separación) dieléctrico-aire. Como son medios dieléctricos que consideraremos ideales, no puede haber allí carga eléctrica libre. Obsérvese que dicha superficie tiene las mismas características eléctricas que una superficie conductora descargada y aislada y, por tanto, es equivalente a ella. Es decir, las propiedades eléctricas del sistema con dieléctrico no se verían modificadas si se coloca una lámina conductora delgada, aislada y sin carga, en la superficie del dieléctrico, separándolo de la región vacía. En consecuencia, el sistema parcialmente relleno es equivalente a la asociación en serie de dos condensadores planos de igual sección S. Uno completamente relleno de un dieléctrico de constante κ = 2 y espesor  , y otro vacío con una separación entre conductores
, y otro vacío con una separación entre conductores 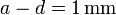 .
.
Las capacidades de los condensadores de la asociación son:
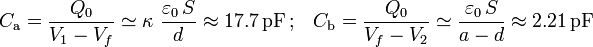
Para obtener el valor de la capacidad equivalente C aplicamos que la carga almacenada en cada uno de los de la asociación en serie es la misma que en el equivalente. Y la diferencia de potencial en éste debe ser la suma de las diferencias de potencial en los de la asociación. Es decir,