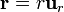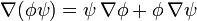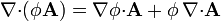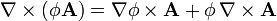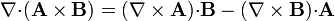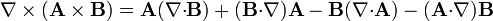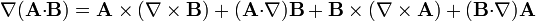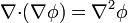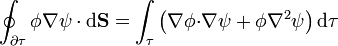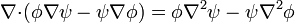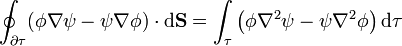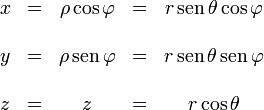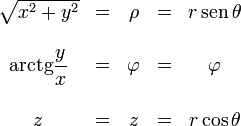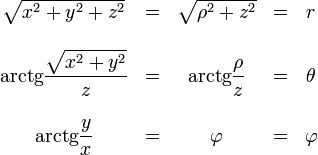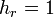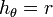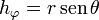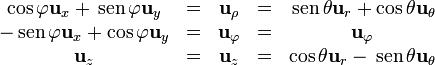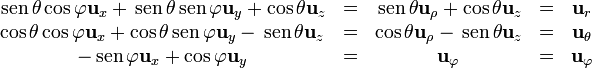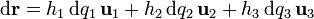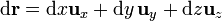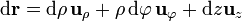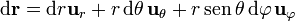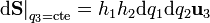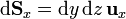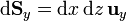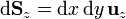Tabla de cálculo vectorial

De Laplace

(Diferencias entre revisiones)

Revisión de 10:50 25 jul 2008

Contenido

1 Álgebra del operador nabla
2 Relación entre los sistemas de coordenadas
3 Vector de posición
4 Factores de escala
5 Relación entre bases vectoriales
6 Diferenciales

1 Álgebra del operador nabla

1.1 Aplicación sobre productos

1.1.1 De dos campos escalares

$\nabla(\phi\psi) = \psi \,\nabla\phi+\phi\,\nabla\psi$

1.1.2 De un campo escalar por uno vectorial

$\nabla{\cdot}(\phi\mathbf{A}) = \nabla\phi {\cdot}\mathbf{A}+\phi\,\nabla{\cdot}\mathbf{A}$

$\nabla\times(\phi\mathbf{A}) = \nabla\phi\times\mathbf{A}+\phi\,\nabla\times\mathbf{A}$

1.1.3 De dos campos vectoriales

$\nabla{\cdot}(\mathbf{A}\times\mathbf{B}) = (\nabla\times\mathbf{A}){\cdot}\mathbf{B}-(\nabla\times\mathbf{B}){\cdot}\mathbf{A}$

$\nabla\times(\mathbf{A}\times\mathbf{B}) = \mathbf{A}(\nabla{\cdot}\mathbf{B})+ (\mathbf{B}{\cdot}\nabla)\mathbf{A}-\mathbf{B}(\nabla{\cdot}\mathbf{A})-(\mathbf{A}{\cdot}\nabla)\mathbf{B}$

$\nabla(\mathbf{A}{\cdot}\mathbf{B}) = \mathbf{A}\times(\nabla\times\mathbf{B})+(\mathbf{A}{\cdot}\nabla)\mathbf{B}+\mathbf{B}\times(\nabla\times\mathbf{A})+(\mathbf{B}{\cdot}\nabla)\mathbf{A}$

1.2 Operadores de segundo orden

$\nabla{\cdot}(\nabla\phi) = \nabla^2\phi$

$\nabla\times(\nabla\phi) = \mathbf{0}$

$\nabla{\cdot}(\nabla\times\mathbf{A}) = 0$

$\nabla\times(\nabla\times\mathbf{A}) = \nabla(\nabla{\cdot}\mathbf{A})-\nabla^2\mathbf{A}$

1.3 Identidades de Green

1.3.1 Primera

1.3.1.1 En forma diferencial

$\nabla{\cdot}(\phi\nabla\psi)=\nabla\phi{\cdot}\nabla\psi+\phi\nabla^2\psi$

1.3.1.2 En forma integral

$\oint_{\partial\tau}\phi\nabla\psi\cdot\mathrm{d}\mathbf{S}=\int_\tau\left(\nabla\phi{\cdot}\nabla\psi+\phi\nabla^2\psi\right)\mathrm{d}\tau$

1.3.2 Segunda

1.3.2.1 En forma diferencial

$\nabla{\cdot}(\phi\nabla\psi-\psi\nabla\phi)=\phi\nabla^2\psi-\psi\nabla^2\phi$

1.3.2.2 En forma integral

$\oint_{\partial\tau}(\phi\nabla\psi-\psi\nabla\phi)\cdot\mathrm{d}\mathbf{S}=\int_\tau\left(\phi\nabla^2\psi-\psi\nabla^2\phi\right)\mathrm{d}\tau$

2 Relación entre los sistemas de coordenadas

2.1 De cartesianas a otros sistemas

$\begin{array}{ccccc} x & = & \rho\cos\varphi & =& r\,\operatorname{sen}\,\theta\cos\varphi \\&&&&\\ y &=&\rho\,\operatorname{sen}\,\varphi & = & r\,\operatorname{sen}\,\theta\,\operatorname{sen}\,\varphi\\&&&&\\ z &=& z &=& r\cos\theta\end{array}$

2.2 De cilíndricas a otros sistemas

$\begin{array}{ccccc}\sqrt{x^2+y^2} &=& \rho &=& r\,\operatorname{sen}\,\theta \\ &&&& \\ \operatorname{arctg}\displaystyle\frac{y}{x} &=& \varphi &=& \varphi \\&&&&\\ z &=& z&=& r\cos\theta\end{array}$

2.3 De esféricas a otros sistemas

$\begin{array}{ccccc}\sqrt{x^2+y^2+z^2}&= & \sqrt{\rho^2+z^2}&=& r \\&&&&\\ \operatorname{arctg}\displaystyle\frac{\sqrt{x^2+y^2}}{z} & = & \operatorname{arctg}\displaystyle\frac{\rho}{z}&=& \theta \\&&&&\\ \operatorname{arctg}\displaystyle\frac{y}{x}& =& \varphi &=& \varphi\end{array}$

3 Vector de posición

3.1 En cartesianas

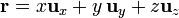
$\mathbf{r}=x\mathbf{u}_{x}+y\,\mathbf{u}_{y}+z\mathbf{u}_{z}$

3.2 En cilíndricas

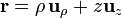
$\mathbf{r}=\rho\,\mathbf{u}_{\rho}+z\mathbf{u}_{z}$

3.3 En esféricas

$\mathbf{r}=r\mathbf{u}_{r}$

4 Factores de escala

4.1 Definición

$h_i=\left|\frac{\partial \mathbf{r}}{\partial q_i}\right|$

4.2 Cartesianas

$h_x=1\,$ $h_y=1\,$ $h_z=1\,$

4.3 Cilíndricas

$h_\rho=1\,$ $h_\varphi=\rho$ $h_z=1\,$

4.4 Esféricas

$h_r=1\,$ $h_\theta=r\,$ $h_\varphi=r\,\operatorname{sen}\,\theta$

5 Relación entre bases vectoriales

5.1 De cartesianas a otro sistema

$\begin{array}{ccccc} \mathbf{u}_{x} & = & \cos\varphi\mathbf{u}_{\rho}-\,\operatorname{sen}\,\varphi\mathbf{u}_{\varphi} & = & \,\operatorname{sen}\,\theta\cos\varphi\mathbf{u}_{r}+\cos\theta\cos\varphi\mathbf{u}_{\theta}-\,\operatorname{sen}\,\varphi\mathbf{u}_{\varphi} \\ \mathbf{u}_{y} & = & \,\operatorname{sen}\,\varphi\mathbf{u}_{\rho}+\cos\varphi\mathbf{u}_{\varphi} & = & \,\operatorname{sen}\,\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{r}+\cos\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{\theta}+\cos\varphi\mathbf{u}_{\varphi} \\ \mathbf{u}_{z} & = & \mathbf{u}_{z} & = & \cos\theta\mathbf{u}_{r}-\,\operatorname{sen}\,\theta\mathbf{u}_{\theta} \end{array}$

5.2 De cilíndricas a otro sistema

$\begin{array}{ccccc} \cos\varphi\mathbf{u}_{x}+\,\operatorname{sen}\,\varphi\mathbf{u}_{y} & = & \mathbf{u}_{\rho} & = & \,\operatorname{sen}\,\theta\mathbf{u}_{r}+\cos\theta\mathbf{u}_{\theta} \\ -\,\operatorname{sen}\,\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y} & = & \mathbf{u}_{\varphi}& = & \mathbf{u}_{\varphi} \\ \mathbf{u}_{z} & = & \mathbf{u}_{z} & = & \cos\theta\mathbf{u}_{r}-\,\operatorname{sen}\,\theta\mathbf{u}_{\theta}\\ \end{array}$

5.3 De esféricas a otro sistema

$\begin{array}{ccccc} \,\operatorname{sen}\,\theta\cos\varphi\mathbf{u}_{x}+\,\operatorname{sen}\,\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{y}+\cos\theta\mathbf{u}_{z} & = & \,\operatorname{sen}\,\theta\mathbf{u}_{\rho}+\cos\theta\mathbf{u}_{z} & = & \mathbf{u}_{r} \\ \cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\,\operatorname{sen}\,\varphi\mathbf{u}_{y}-\,\operatorname{sen}\,\theta\mathbf{u}_{z} & = &\cos\theta\mathbf{u}_{\rho}-\,\operatorname{sen}\,\theta\mathbf{u}_{z} & = & \mathbf{u}_{\theta} \\ -\,\operatorname{sen}\,\varphi\mathbf{u}_{x}+\cos\varphi\mathbf{u}_{y} & = & \mathbf{u}_{\varphi}& = & \mathbf{u}_{\varphi} \\ \end{array}$

6 Diferenciales

6.1 De camino

6.1.1 Para coordenadas ortogonales

$\mathrm{d}\mathbf{r}=h_1\,\mathrm{d}q_1\,\mathbf{u}_{1}+h_2\,\mathrm{d}q_2\,\mathbf{u}_{2}+h_3\,\mathrm{d}q_3\,\mathbf{u}_{3}$

6.1.2 En cartesianas

$\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{u}_{x}+\mathrm{d}y\,\mathbf{u}_{y}+\mathrm{d}z\mathbf{u}_{z}$

6.1.3 En cilíndricas

$\mathrm{d}\mathbf{r}=\mathrm{d}\rho\,\mathbf{u}_{\rho}+\rho\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}+\mathrm{d}z\mathbf{u}_{z}$

6.1.4 En esféricas

$\mathrm{d}\mathbf{r}=\mathrm{d}r\mathbf{u}_{r}+r\,\mathrm{d}\theta\,\mathbf{u}_{\theta}+r\,\operatorname{sen}\,\theta\,\mathrm{d}\varphi\,\mathbf{u}_{\varphi}$

6.2 De superficie

6.2.1 Para coordenadas ortogonales

$\left.\mathrm{d}\mathbf{S}\right|_{q_3=\mathrm{cte}}= h_1 h_2 \mathrm{d}q_1 \mathrm{d}q_2 \mathbf{u}_{3}$

6.2.2 En cartesianas

$\mathrm{d}\mathbf{S}_x=\mathrm{d}y\,\mathrm{d}z\,\mathbf{u}_{x}$

$\mathrm{d}\mathbf{S}_y=\mathrm{d}x\,\mathrm{d}z\,\mathbf{u}_{y}$

$\mathrm{d}\mathbf{S}_z=\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_{z}$

@@ Línea 124: / Línea 124: @@
 :<math>\left.\mathrm{d}\mathbf{S}\right|_{q_3=\mathrm{cte}}= h_1 h_2 \mathrm{d}q_1 \mathrm{d}q_2 \mathbf{u}_{3}</math>
 ====En cartesianas====
+:<math>\mathrm{d}\mathbf{S}_x=\mathrm{d}y\,\mathrm{d}z\,\mathbf{u}_{x}</math>
+:<math>\mathrm{d}\mathbf{S}_y=\mathrm{d}x\,\mathrm{d}z\,\mathbf{u}_{y}</math>
+:<math>\mathrm{d}\mathbf{S}_z=\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_{z}</math>
 ====En cilíndricas====
 ====En esféricas====