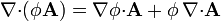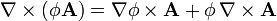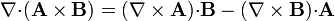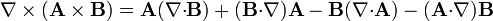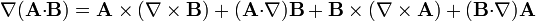Tabla de cálculo vectorial
De Laplace
(Diferencias entre revisiones)
(→=De dos campos escalares) |
(→De dos campos vectoriales) |
||
| Línea 7: | Línea 7: | ||
:<math>\nabla\times(\phi\mathbf{A}) = \nabla\phi\times\mathbf{A}+\phi\,\nabla\times\mathbf{A}</math> | :<math>\nabla\times(\phi\mathbf{A}) = \nabla\phi\times\mathbf{A}+\phi\,\nabla\times\mathbf{A}</math> | ||
====De dos campos vectoriales==== | ====De dos campos vectoriales==== | ||
| - | :<math>\nabla{\cdot}(\mathbf{A}\times\mathbf{B}) | + | :<math>\nabla{\cdot}(\mathbf{A}\times\mathbf{B}) = |
(\nabla\times\mathbf{A}){\cdot}\mathbf{B}-(\nabla\times\mathbf{B}){\cdot}\mathbf{A}</math> | (\nabla\times\mathbf{A}){\cdot}\mathbf{B}-(\nabla\times\mathbf{B}){\cdot}\mathbf{A}</math> | ||
| - | :<math>\nabla\times(\mathbf{A}\times\mathbf{B}) | + | :<math>\nabla\times(\mathbf{A}\times\mathbf{B}) = \mathbf{A}(\nabla{\cdot}\mathbf{B})+ |
(\mathbf{B}{\cdot}\nabla)\mathbf{A}-\mathbf{B}(\nabla{\cdot}\mathbf{A})-(\mathbf{A}{\cdot}\nabla)\mathbf{B}</math> | (\mathbf{B}{\cdot}\nabla)\mathbf{A}-\mathbf{B}(\nabla{\cdot}\mathbf{A})-(\mathbf{A}{\cdot}\nabla)\mathbf{B}</math> | ||
| - | :<math>\nabla(\mathbf{A}{\cdot}\mathbf{B}) | + | :<math>\nabla(\mathbf{A}{\cdot}\mathbf{B}) = \mathbf{A}\times(\nabla\times\mathbf{B})+(\mathbf{A}{\cdot}\nabla)\mathbf{B}+\mathbf{B}\times(\nabla\times\mathbf{A})+(\mathbf{B}{\cdot}\nabla)\mathbf{A}</math> |
Revisión de 15:41 22 jul 2008
Contenido |