Entrar Página Discusión Historial Go to the site toolbox

Tubo con dos cámaras de gas

De Laplace

(Diferencias entre revisiones)
(→Fuerza)
Línea 19: Línea 19:
Sus presiones, sin embargo, son diferentes. Aunque en las dos cámaras se encuentra la misma masa de gas, el número de moles es diferente. Obtenemos la cantidad de moles dividiendo por el peso molecular. Para el [http://es.wikipedia.org/wiki/Dihidr%C3%B3geno hidrógeno]
Sus presiones, sin embargo, son diferentes. Aunque en las dos cámaras se encuentra la misma masa de gas, el número de moles es diferente. Obtenemos la cantidad de moles dividiendo por el peso molecular. Para el [http://es.wikipedia.org/wiki/Dihidr%C3%B3geno hidrógeno]
-
<center><math>P_m = 2.016\frac{\mathrm{g}}{\mathrm{mol}\qquad\Rightarrow\qquad n_1 = \frac{m}{P_m} = 1.984\,\mathrm{mol}</math></center>
+
<center><math>P_m = 2.016\frac{\mathrm{g}}{\mathrm{mol}}\qquad\Rightarrow\qquad n_1 = \frac{m}{P_m} = 1.984\,\mathrm{mol}</math></center>
y para el [http://es.wikipedia.org/wiki/Dinitr%C3%B3geno nitrógeno]
y para el [http://es.wikipedia.org/wiki/Dinitr%C3%B3geno nitrógeno]
-
<center><math>P_m = 28.0134\frac{\mathrm{g}}{\mathrm{mol}\qquad\Rightarrow\qquad n_2 = \frac{m}{P_m} = 0.143\,\mathrm{mol}</math></center>
+
<center><math>P_m = 28.0134\frac{\mathrm{g}}{\mathrm{mol}}\qquad\Rightarrow\qquad n_2 = \frac{m}{P_m} = 0.143\,\mathrm{mol}</math></center>
En estas fórmulas se podían haber usado como masas moleculares 2&thinsp;g/mol y 28&thinsp;g/mol, y el resultado sería bastante aproximado al correcto.
En estas fórmulas se podían haber usado como masas moleculares 2&thinsp;g/mol y 28&thinsp;g/mol, y el resultado sería bastante aproximado al correcto.

Revisión de 20:23 15 feb 2012

1 Enunciado

Se tiene una cámara cilíndrica horizontal de 20 cm de diámetro y 60 cm de longitud de paredes rígidas. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente está fijado con pernos. En la cámara de la izquierda hay 4.0 g de H2 gaseoso y en la de la derecha 4.0 g de N2. Los dos gases y el ambiente que los rodea están a 25°C.

  1. Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central.
  2. Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas

2 Fuerza

Sea 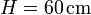H = 60\,\mathrm{cm} la longitud del tubo y

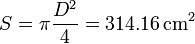
S=\pi\frac{D^2}{4}= 314.16\,\mathrm{cm}^2

su sección. El volumen cada gas es el mismo, la mitad del del cilindro

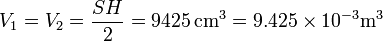
V_1 = V_2 = \frac{SH}{2} = 9425\,\mathrm{cm}^3 = 9.425\times 10^{-3}\mathrm{m}^3

y también son iguales sus temperaturas

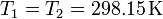
T_1 = T_2 = 298.15\,\mathrm{K}

Sus presiones, sin embargo, son diferentes. Aunque en las dos cámaras se encuentra la misma masa de gas, el número de moles es diferente. Obtenemos la cantidad de moles dividiendo por el peso molecular. Para el hidrógeno

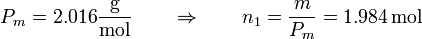
P_m = 2.016\frac{\mathrm{g}}{\mathrm{mol}}\qquad\Rightarrow\qquad n_1 = \frac{m}{P_m} = 1.984\,\mathrm{mol}

y para el nitrógeno

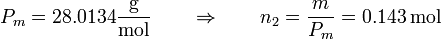
P_m = 28.0134\frac{\mathrm{g}}{\mathrm{mol}}\qquad\Rightarrow\qquad n_2 = \frac{m}{P_m} = 0.143\,\mathrm{mol}

En estas fórmulas se podían haber usado como masas moleculares 2 g/mol y 28 g/mol, y el resultado sería bastante aproximado al correcto.

Esto nos da la presión del hidrógeno

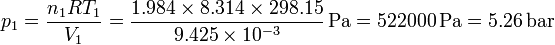
p_1 = \frac{n_1 R T_1}{V_1}= \frac{1.984\times 8.314\times 298.15}{9.425\times 10^{-3}}\,\mathrm{Pa} = 522000\,\mathrm{Pa} = 5.26\,\mathrm{bar}

y la del nitrógeno

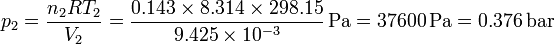
p_2 = \frac{n_2 R T_2}{V_2}= \frac{0.143\times 8.314\times 298.15}{9.425\times 10^{-3}}\,\mathrm{Pa} = 37600\,\mathrm{Pa} = 0.376\,\mathrm{bar}

Vemos que la presión es mucho mayor en el lado del hidrógeno, por haber muchos más moles de este gas.

3 Posición de equilibrio

Obtenido de "http://tesla.us.es/wiki/index.php/Tubo_con_dos_c%C3%A1maras_de_gas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace