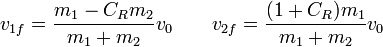Colisión parcialmente inelástica
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula de masa <math>m_1</math> y que se mueve con velocidad <math>v_0</math> impacta frontalmente con una de masa <math>m_2</math> que se encuentra en rep…') |
|||
| Línea 7: | Línea 7: | ||
==Velocidades finales== | ==Velocidades finales== | ||
| + | Las velocidades finales las obtenemos de dos ecuaciones: | ||
| + | |||
| + | ;La conservación de la cantidad de movimiento: Suponiendo que tras el choque ambas partículas se mueven sobre la recta por la que venía el proyectil inicial, esta ley nos da | ||
| + | |||
| + | <center><math>m_1v_0 = m_1v_{1f}+m_2v_{2f}\,</math></center> | ||
| + | |||
| + | ;El coeficiente de restitución es conocido: Este coeficiente relaciona la velocidad relativa de alejamiento con la de acercamiento | ||
| + | |||
| + | <center><math>C_R=\frac{v_{2f}-v_{1f}}{v_{1i}-v_{2i}}\qquad\Rightarrow\qquad v_{2f}-v_{1f}=C_Rv_0</math></center> | ||
| + | |||
| + | Estos da un sistema de dos ecuaciones con dos incógnitas, con solución general | ||
| + | |||
| + | <center><math>v_{1f}=\frac{m_1-C_Rm_2}{m_1+m_2}v_0\qquad v_{2f}=\frac{(1+C_R)m_1}{m_1+m_2}v_0</math></center> | ||
==Disipación de energía cinética== | ==Disipación de energía cinética== | ||
==Límite de los resultados== | ==Límite de los resultados== | ||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
Revisión de 21:41 14 dic 2011
Contenido |
1 Enunciado
Una partícula de masa m1 y que se mueve con velocidad v0 impacta frontalmente con una de masa m2 que se encuentra en reposo. El coeficiente de restitución vale CR = 0.5
- Halle las velocidades finales de las dos partículas
- Calcule la cantidad de energía cinética disipada en el proceso.
- ¿A qué tienden los resultados anteriores si
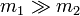? ¿Y si 
?
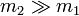2 Velocidades finales
Las velocidades finales las obtenemos de dos ecuaciones:
- La conservación de la cantidad de movimiento
- Suponiendo que tras el choque ambas partículas se mueven sobre la recta por la que venía el proyectil inicial, esta ley nos da
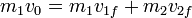
- El coeficiente de restitución es conocido
- Este coeficiente relaciona la velocidad relativa de alejamiento con la de acercamiento
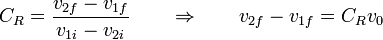
Estos da un sistema de dos ecuaciones con dos incógnitas, con solución general
