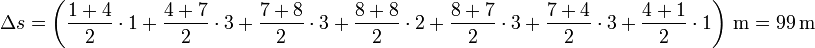Ejemplo de integración numérica
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica <center>[[Archivo:velocidad-circ…') |
|||
| Línea 14: | Línea 14: | ||
==Solución numérica== | ==Solución numérica== | ||
| + | Si conocemos la velocidad instantánea, podemos hallar el desplazamiento a base de sumar los desplazamientos diferenciales | ||
| + | |||
| + | <center><math>\Delta s = \int_0^t v(t)\,\mathrm{d}t</math></center> | ||
| + | |||
| + | Gráficamente, esto equivale a hallar el área bajo la curva de la velocidad frente al tiempo. | ||
| + | |||
| + | Examinando la figura, podemos ver que la curva corta la cuadrícula en los puntos de coordenadas enteras (en el SI) (0,1), (1,4), (4,7), (7,8), (9,8), (12,7), (15,4) y (16,1): | ||
| + | |||
| + | <center>[[Archivo:velocidad-trapecios.png]]</center> | ||
| + | |||
| + | El área bajo la curva puede entonces ser aproximada por una suma de trapecios, siendo la fórmula para el área de cada uno | ||
| + | |||
| + | <center><math>\Delta S = \frac{b+B}{2}h = \frac{v(t_1)+v(t_2)}{2}\Delta t</math></center> | ||
| + | |||
| + | Aplicando esto a nuestro caso obtenemos el desplazamiento aproximado | ||
| + | |||
| + | <center><math>\Delta s = \left(\frac{1+4}{2}\cdot 1+\frac{4+7}{2}\cdot 3+\frac{7+8}{2}\cdot 3+\frac{8+8}{2}\cdot 2 + \frac{8+7}{2}\cdot 3+\frac{7+4}{2}\cdot 3+\frac{4+1}{2}\cdot 1\right)\,\mathrm{m} = 99\,\mathrm{m}</math></center> | ||
==Solución analítica== | ==Solución analítica== | ||
[[Categoría:Problemas de herramientas matemáticas (GIE)]] | [[Categoría:Problemas de herramientas matemáticas (GIE)]] | ||
Revisión de 16:59 4 oct 2011
1 Enunciado
Una partícula se mueve a lo largo de una recta, siendo su velocidad (en el SI) como función del tiempo, la dada por la gráfica
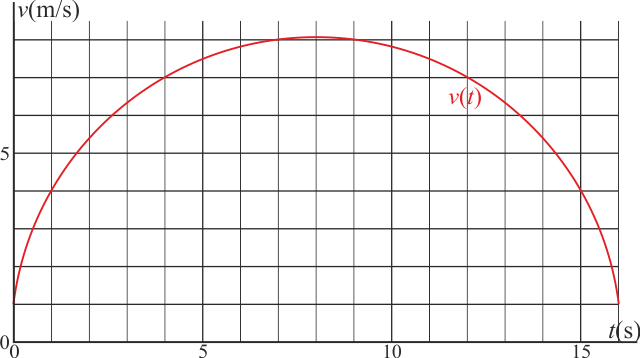
La partícula parte de s = 0.
- Aprovechando los puntos en que la curva cruza la cuadrícula, calcule aproximadamente la posición en que se encontrará la partícula en
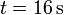 .
.
- Calcule el valor exacto de esta posición, sabiendo que la ley para la velocidad es

- ¿Cuál es el error relativo cometido en el apartado anterior?
2 Solución numérica
Si conocemos la velocidad instantánea, podemos hallar el desplazamiento a base de sumar los desplazamientos diferenciales
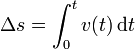
Gráficamente, esto equivale a hallar el área bajo la curva de la velocidad frente al tiempo.
Examinando la figura, podemos ver que la curva corta la cuadrícula en los puntos de coordenadas enteras (en el SI) (0,1), (1,4), (4,7), (7,8), (9,8), (12,7), (15,4) y (16,1):
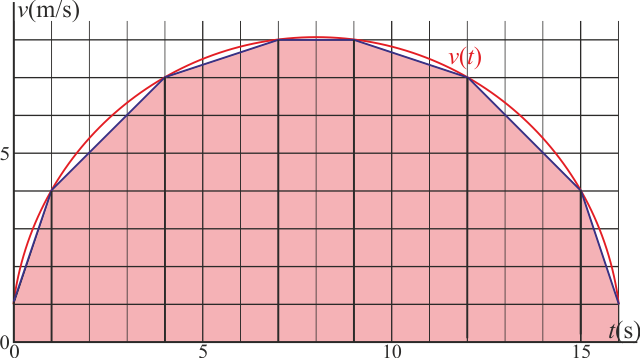
El área bajo la curva puede entonces ser aproximada por una suma de trapecios, siendo la fórmula para el área de cada uno
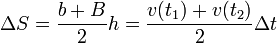
Aplicando esto a nuestro caso obtenemos el desplazamiento aproximado