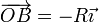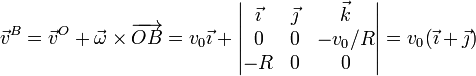4.8. Rodadura permanente de un disco
De Laplace
(Diferencias entre revisiones)
(→Velocidades) |
|||
| Línea 20: | Línea 20: | ||
:por lo que su velocidad vale | :por lo que su velocidad vale | ||
| - | <center><math>\vec{v}^A = \vec{v}^O +\vec{\omega}\times\overrightarrow{OA}=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -v_0/R \\ 0 & -v_0 & 0 \end{matrix}\right| = \vec{0}</math></center> | + | <center><math>\vec{v}^A = \vec{v}^O +\vec{\omega}\times\overrightarrow{OA}=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -v_0/R \\ 0 & -R & 0 \end{matrix}\right| = \vec{0}</math></center> |
| + | |||
| + | ;Punto B: | ||
| + | |||
| + | <center><math>\overrightarrow{OB}=R\vec{\imath}</math>{{qquad}}{{qquad}}<math>\vec{v}^B = \vec{v}^O +\vec{\omega}\times\overrightarrow{OB}=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -v_0/R \\ R & 0 & 0 \end{matrix}\right| = v_0(\vec{\imath}-\vec{\jmath})</math></center> | ||
| + | |||
| + | ;Punto C: | ||
| + | |||
| + | <center><math>\overrightarrow{OC}=R\vec{\jmath}</math>{{qquad}}{{qquad}}<math>\vec{v}^C = \vec{v}^O +\vec{\omega}\times\overrightarrow{OA}=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -v_0/R \\ 0 & R & 0 \end{matrix}\right| = 2v_0\vec{\imath}</math></center> | ||
| + | |||
| + | ;Punto D: | ||
| + | |||
| + | <center><math>\overrightarrow{OB}=-R\vec{\imath}</math>{{qquad}}{{qquad}}<math>\vec{v}^B = \vec{v}^O +\vec{\omega}\times\overrightarrow{OB}=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -v_0/R \\ -R & 0 & 0 \end{matrix}\right| = v_0(\vec{\imath}+\vec{\jmath})</math></center> | ||
| + | |||
==Aceleraciones== | ==Aceleraciones== | ||
[[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]] | [[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]] | ||
Revisión de 21:25 13 nov 2010
1 Enunciado
La rodadura permanente de un disco de radio R sobre una superficie horizontal puede describirse mediante el campo de velocidades
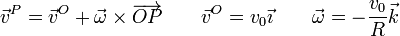
donde la superficie horizontal se encuentra en y = − R.
- Determine, para un instante dado, la velocidades de los puntos A, B, C y D situados en los cuatro cuadrantes del disco.
- Calcule la aceleración de estos puntos para el mismo instante, suponiendo v0 = cte.
2 Velocidades
Para cada uno de los puntos, basta aplicar la fórmula correspondiente
- Punto A
- Su vector de posición relativa es
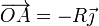
- por lo que su velocidad vale
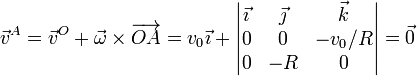
- Punto B
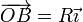
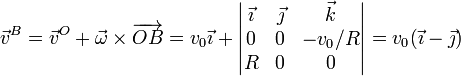
- Punto C
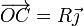
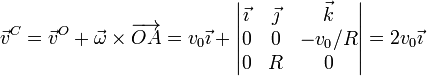
- Punto D