Independencia de la parametrización
De Laplace
(→Introducción) |
(→Introducción) |
||
| Línea 4: | Línea 4: | ||
Si lo que tenemos es un movimiento, dado por su ecuación horaria <math>\vec{r}(t)</math>, ¿cómo podemos saber si una propiedad concreta, calculada a partir de ella, es una propiedad geométrica o es dependiente del estado de movimiento? | Si lo que tenemos es un movimiento, dado por su ecuación horaria <math>\vec{r}(t)</math>, ¿cómo podemos saber si una propiedad concreta, calculada a partir de ella, es una propiedad geométrica o es dependiente del estado de movimiento? | ||
| - | La respuesta es que hay que establecer si dicha propiedad es independiente de la parametrización. Esto es, nos imaginamos que la partícula recorre los mismos puntos a un ritmo diferente, de forma que la ecuación horaria es ahora <math>\vec{r}(T | + | La respuesta es que hay que establecer si dicha propiedad es independiente de la parametrización. Esto es, nos imaginamos que la partícula recorre los mismos puntos a un ritmo diferente, de forma que la ecuación horaria es ahora <math>\vec{r}(T)</math>, siendo <math>T</math> una nueva variable temporal. Si calculando la propiedad empleando la nueva variable resulta el mismo valor que con la original, entonces es una propiedad geométrica, esto es, no depende de cómo de rápido se recorre la curva. |
En lo que sigue indicaremos las principales propiedades geométricas que aparecen en la cinemática de la partícula. | En lo que sigue indicaremos las principales propiedades geométricas que aparecen en la cinemática de la partícula. | ||
Revisión de 15:48 16 sep 2010
Contenido |
1 Introducción
A la hora de estudiar la cinemática de la partícula, surgen conceptos puramente geométricos que no dependen de la ley horaria del movimiento de una partícula (esto es, de con qué celeridad pasa de un punto a otro). Otros, en cambio, sí dependen. Por ejemplo, la velocidad instantánea es claramente dependiente del estado de movimiento. Sin embargo, el vector tangente a la trayectoria, que nos indica hacia donde se dirige la partícula, y que se calcula a partir de la velocidad instantánea, no depende de si la partícula se mueve lento o rápido. La dirección del movimiento es una propiedad geométrica.
Si lo que tenemos es un movimiento, dado por su ecuación horaria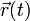 
, ¿cómo podemos saber si una propiedad concreta, calculada a partir de ella, es una propiedad geométrica o es dependiente del estado de movimiento?
La respuesta es que hay que establecer si dicha propiedad es independiente de la parametrización. Esto es, nos imaginamos que la partícula recorre los mismos puntos a un ritmo diferente, de forma que la ecuación horaria es ahora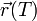 
, siendo T una nueva variable temporal. Si calculando la propiedad empleando la nueva variable resulta el mismo valor que con la original, entonces es una propiedad geométrica, esto es, no depende de cómo de rápido se recorre la curva.
En lo que sigue indicaremos las principales propiedades geométricas que aparecen en la cinemática de la partícula.
