Esfera conductora rellena de dieléctrico con hueco
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Enunciado) |
||
| Línea 2: | Línea 2: | ||
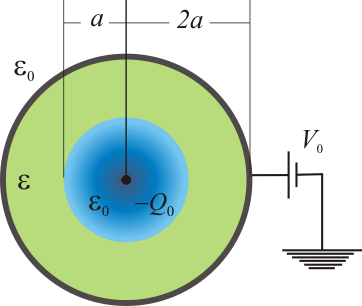
Una superficie esférica conductora ideal de pequeño espesor y radio $2a$ está rellena de un medio dieléctrico ideal homogéneo de permitividad <math>\varepsilon=5\varepsilon_0/2</math>, en cuyo centro hay un hueco de radio $a$. Estando la superficie conductora conectada a un potencial <math>V_0</math>, el hueco es llenado con una nube de electrones cuya carga total es <math>-Q_0</math>. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones: | Una superficie esférica conductora ideal de pequeño espesor y radio $2a$ está rellena de un medio dieléctrico ideal homogéneo de permitividad <math>\varepsilon=5\varepsilon_0/2</math>, en cuyo centro hay un hueco de radio $a$. Estando la superficie conductora conectada a un potencial <math>V_0</math>, el hueco es llenado con una nube de electrones cuya carga total es <math>-Q_0</math>. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones: | ||
| - | [[Archivo:P1_sep_09_10_0.gif|right]]# Determine los campos <math>\mathbf{E}</math>, <math>\mathbf{D}</math> y <math>\mathbf{P}</math>, tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco. | + | [[Archivo:P1_sep_09_10_0.gif|right]] |
| + | |||
| + | # Determine los campos <math>\mathbf{E}</math>, <math>\mathbf{D}</math> y <math>\mathbf{P}</math>, tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco. | ||
# Halle la densidad de carga libre y la total en la interfaz <math>r=a</math> y en la cara interior y la exterior de la superficie conductora, antes y después de llenar el hueco. | # Halle la densidad de carga libre y la total en la interfaz <math>r=a</math> y en la cara interior y la exterior de la superficie conductora, antes y después de llenar el hueco. | ||
# Calcule la energía electrostática almacenada en el sistema, antes y después de llenar el hueco. | # Calcule la energía electrostática almacenada en el sistema, antes y después de llenar el hueco. | ||
[[Categoría:Problemas de materiales dieléctricos]] | [[Categoría:Problemas de materiales dieléctricos]] | ||
Revisión de 11:47 10 sep 2010
Enunciado
Una superficie esférica conductora ideal de pequeño espesor y radio $2a$ está rellena de un medio dieléctrico ideal homogéneo de permitividad 
, en cuyo centro hay un hueco de radio $a$. Estando la superficie conductora conectada a un potencial V0, el hueco es llenado con una nube de electrones cuya carga total es − Q0. Suponiendo que esta carga se distribuye uniformemente en el hueco y que en el medio dieléctrico no hay carga libre, resuelva las siguientes cuestiones:
- Determine los campos
, 
y 
, tanto en el interior como en el exterior de la esfera, antes y después de introducir la carga eléctrica en el hueco.
- Halle la densidad de carga libre y la total en la interfaz r = a y en la cara interior y la exterior de la superficie conductora, antes y después de llenar el hueco.
- Calcule la energía electrostática almacenada en el sistema, antes y después de llenar el hueco.
