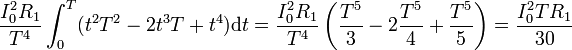Pulso de corriente inducida
De Laplace
(Diferencias entre revisiones)
(→Energía disipada en el hilo) |
(→Energía disipada en el hilo) |
||
| Línea 27: | Línea 27: | ||
La energía disipada se calcula de forma análoga a partir de la potencia | La energía disipada se calcula de forma análoga a partir de la potencia | ||
| - | <center><math>W_d = \int_0^T I^2R_1\,\mathrm{d}t = \frac{I_0^2R_1}{T^4}\int_0^T (tT-t^2)^2\mathrm{d}t =</math><math>\ \frac{I_0^2R_1}{T^4}\int_0^T (t^2T^2-2t^3T+t^4)\mathrm{d}t=\frac{I_0^2R_1}{T^4}\left(\frac{T^5}{3}-2\frac{T^5}{4}+\frac{T^5}{5}\right) = \frac{I_0^2TR_1}{30}</math></center> | + | <center><math>W_d = \int_0^T I^2R_1\,\mathrm{d}t = \frac{I_0^2R_1}{T^4}\int_0^T (tT-t^2)^2\mathrm{d}t =</math><math>\,\,\frac{I_0^2R_1}{T^4}\int_0^T (t^2T^2-2t^3T+t^4)\mathrm{d}t=\frac{I_0^2R_1}{T^4}\left(\frac{T^5}{3}-2\frac{T^5}{4}+\frac{T^5}{5}\right) = \frac{I_0^2TR_1}{30}</math></center> |
==Corriente inducida== | ==Corriente inducida== | ||
Revisión de 14:39 4 sep 2010
Contenido |
1 Enunciado
Por un hilo rectilíneo de gran longitud y resistencia eléctrica R1 circula una corriente variable en el tiempo, tal que su valor es
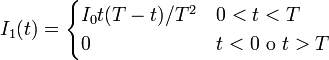
- Halle la carga que pasa por un punto del hilo entre
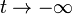y 
.
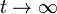- Calcule la energía disipada en el cable en el mismo tiempo.
- Junto al cable y coplanaria con él se encuentra una pequeña espira cuadrada de lado a con su centro situado a una distancia b (
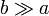) del hilo. Esta espira posee resistencia R2 y autoinducción despreciable. Calcule la corriente inducida en esta espira como función del tiempo.
- Halle la carga que pasa por un punto de la espira entre 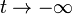y .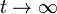
- Calcule la energía disipada en la espira en el mismo tiempo.
2 Carga que recorre el hilo
La carga que pasa por una sección del hilo en un tiempo dt es
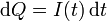
Por lo que la carga total que pasa vale
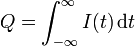
En este caso, tenemos que la corriente es nula salvo en el intervalo 0 < t < T por lo que el cálculo se reduce a
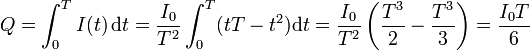
3 Energía disipada en el hilo
La energía disipada se calcula de forma análoga a partir de la potencia
