Pulso de corriente inducida
De Laplace
(Diferencias entre revisiones)
(Página creada con 'Por un hilo rectilíneo de gran longitud y resistencia eléctrica <math>R_1</math> circula una corriente variable en el tiempo, tal que su valor es <center><math>I_1(t) = \begi…') |
|||
| Línea 1: | Línea 1: | ||
| + | ==Enucniado== | ||
Por un hilo rectilíneo de gran longitud y resistencia eléctrica <math>R_1</math> circula una corriente variable en el tiempo, tal | Por un hilo rectilíneo de gran longitud y resistencia eléctrica <math>R_1</math> circula una corriente variable en el tiempo, tal | ||
que su valor es | que su valor es | ||
| Línea 10: | Línea 11: | ||
# Calcule la energía disipada en la espira en el mismo tiempo. | # Calcule la energía disipada en la espira en el mismo tiempo. | ||
| + | ==Carga que recorre el hilo== | ||
| + | ==Energía disipada en el hilo== | ||
| + | ==Corriente inducida== | ||
| + | ==Carga que recorre la espira== | ||
| + | ==Energía disipada en la espira== | ||
[[Categoría:Problemas de corriente eléctrica]] | [[Categoría:Problemas de corriente eléctrica]] | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
Revisión de 10:54 4 sep 2010
Contenido |
1 Enucniado
Por un hilo rectilíneo de gran longitud y resistencia eléctrica R1 circula una corriente variable en el tiempo, tal que su valor es
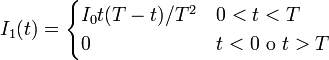
- Halle la carga que pasa por un punto del hilo entre
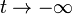y 
.
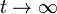- Calcule la energía disipada en el cable en el mismo tiempo.
- Junto al cable y coplanaria con él se encuentra una pequeña espira cuadrada de lado a con su centro situado a una distancia b (
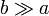) del hilo. Esta espira posee resistencia R2 y autoinducción despreciable. Calcule la corriente inducida en esta espira como función del tiempo.
- Halle la carga que pasa por un punto de la espira entre 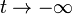y .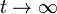
- Calcule la energía disipada en la espira en el mismo tiempo.
