Problemas de corriente eléctrica
De Laplace
(Diferencias entre revisiones)
| Línea 4: | Línea 4: | ||
<center><math>\mathbf{v} = v_0\left(1-\frac{\rho^2}{a^2}\right)\mathbf{u}_{z}</math></center> | <center><math>\mathbf{v} = v_0\left(1-\frac{\rho^2}{a^2}\right)\mathbf{u}_{z}</math></center> | ||
| - | El líquido posee una densidad de carga uniforme | + | El líquido posee una densidad de carga uniforme <math>\rho_0</math>, de forma que la densidad de corriente es <math>\mathbf{J} = \rho_0\mathbf{v}</math>. En el exterior del tubo no hay corriente. |
# Calcule la intensidad de corriente que atraviesa una sección por la tubería. | # Calcule la intensidad de corriente que atraviesa una sección por la tubería. | ||
# Si se desea que por la superficie del tubo circule una corriente superficial <math>\mathbf{K}</math>, de forma que la corriente total sea nula, ¿cuánto debe valer <math>\mathbf{K}</math>? | # Si se desea que por la superficie del tubo circule una corriente superficial <math>\mathbf{K}</math>, de forma que la corriente total sea nula, ¿cuánto debe valer <math>\mathbf{K}</math>? | ||
| + | |||
| + | ===[[Velocidad de arrastre]]=== | ||
| + | Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA. | ||
Revisión de 19:23 4 jun 2008
1 Flujo de líquido por una tubería
Por el interior de una tubería cilíndrica de radio $a$ fluye un líquido con una velocidad, dependiente de la distancia al eje, ρ, como
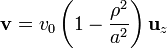
El líquido posee una densidad de carga uniforme ρ0, de forma que la densidad de corriente es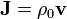 
. En el exterior del tubo no hay corriente.
- Calcule la intensidad de corriente que atraviesa una sección por la tubería.
- Si se desea que por la superficie del tubo circule una corriente superficial
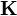, de forma que la corriente total sea nula, ¿cuánto debe valer ?
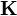2 Velocidad de arrastre
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
