Bobina con dos bobinas interiores
De Laplace
(→Matriz de inducción) |
(→Matriz de inducción) |
||
| Línea 10: | Línea 10: | ||
==Matriz de inducción== | ==Matriz de inducción== | ||
| + | Un elemento de la matriz de coeficientes de autoinducción e inducción mutua, <math>L_{ik}</math> se calcula como | ||
| + | |||
| + | <center><math>L_{ik}=\frac{\Phi_i}{I_k}</math></center> | ||
| + | |||
| + | siendo <math>\Phi_i</math> el flujo a través de la espira <math>i</math> cuando por la espira <math>j</math> circula una corriente <math>I_j</math> y por el resto no circula corriente alguna. | ||
| + | |||
| + | En este sistema tenemos tres boninas. Denominaremos “1” a la exterior y “2” y “3” a las interiores. Por la simetría de la matriz tenemos | ||
| + | |||
| + | <center><math>L_{12}=L_{21}\,</math>{{qquad}}{{qquad}}<math>L_{13}=L_{31}\,</math>{{qquad}}{{qquad}}<math>L_{23}=L_{23}\,</math></center> | ||
| + | |||
| + | y por la simetría entres la bobinas 2 y 3 tenemos además | ||
| + | |||
| + | <center><math>L_{12}=L_{13}\,</math>{{qquad}}{{qquad}}<math>L_{22}=L_{33}\,</math>{{qquad}}{{qquad}}<math>L_{23}=L_{23}\,</math></center> | ||
| + | |||
| + | lo que nos deja con los siguientes elementos diferentes | ||
| + | |||
| + | <center><math>\mathsf{L}=\begin{pmatrix}L_{11} & L_{12} & L_{12} \\ L_{12}& L_{22} & L_{23} \\ L_{12} & L_{23} & L_{22}\end{pmatrix}</math></center> | ||
| + | |||
Cuando se desprecian los efectos de borde y se supone que una bobina es de gran longitud, el campo magnético que produce es, aproximadamente, | Cuando se desprecian los efectos de borde y se supone que una bobina es de gran longitud, el campo magnético que produce es, aproximadamente, | ||
Revisión de 11:17 29 jun 2010
Contenido |
1 Enunciado
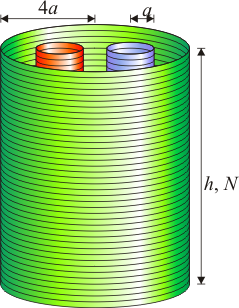
Se tiene un sistema de tres solenoides formado por una bobina de radio 4a, gran longitud h y N vueltas. En el interior de esta bobina se encuentran, separadas, dos bobinas de radio a, misma longitud y mismo número de vueltas. Las ejes de las dos bobinas interiores se encuentran a una distancia 2a del de la grande. Las tres bobinas están arrolladas en el mismo sentido.
- Halle la matriz de coeficientes de autoinducción y de inducción mutua en este sistema. Desprecie los efectos de borde.
- Suponga que se conectan en serie las tres bobinas, de forma que por la bobina exterior circula una corriente + I y por las dos interiores una corriente − I. Exprese el campo magnético en todos los puntos del espacio para esta configuración
- Para el caso anterior, halle la energía magnética almacenada en el sistema. ¿Cuánto vale la autoinducción equivalente de la asociación?
2 Matriz de inducción
Un elemento de la matriz de coeficientes de autoinducción e inducción mutua, Lik se calcula como
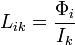
siendo Φi el flujo a través de la espira i cuando por la espira j circula una corriente Ij y por el resto no circula corriente alguna.
En este sistema tenemos tres boninas. Denominaremos “1” a la exterior y “2” y “3” a las interiores. Por la simetría de la matriz tenemos
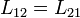
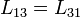
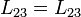
y por la simetría entres la bobinas 2 y 3 tenemos además
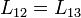
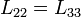
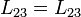
lo que nos deja con los siguientes elementos diferentes

Cuando se desprecian los efectos de borde y se supone que una bobina es de gran longitud, el campo magnético que produce es, aproximadamente,